在探寻因果洞察时,请谨慎解读预测模型
一篇关于因果关系和可解释机器学习的联合文章,作者包括来自微软的 Eleanor Dillon、Jacob LaRiviere、Scott Lundberg、Jonathan Roth 和 Vasilis Syrgkanis。
像 XGBoost 这样的预测性机器学习模型,当与像 SHAP 这样的可解释性工具结合使用时,会变得更加强大。这些工具识别输入特征和预测结果之间最丰富的信息关系,这对于解释模型正在做什么、获得利益相关者的支持以及诊断潜在问题非常有用。人们很容易进一步假设,解释工具还可以识别决策者如果想在未来改变结果,应该操纵哪些特征。然而,在本文中,我们讨论了使用预测模型来指导此类政策选择通常会如何产生误导。
原因在于相关性和因果关系之间的根本区别。SHAP 使预测性机器学习模型捕捉到的相关性变得透明。但是,使相关性透明并不会使它们成为因果关系!所有预测模型都隐含地假设每个人在未来都会保持相同的行为方式,因此相关性模式将保持不变。要理解如果有人开始以不同的方式行事会发生什么,我们需要构建因果模型,这需要做出假设并使用因果分析的工具。
用户留存示例
假设我们的任务是构建一个模型,预测客户是否会续订其产品订阅。假设经过一番挖掘,我们设法获得了八个对于预测客户流失很重要的特征:客户折扣、广告支出、客户的每月使用量、上次升级、客户报告的错误、与客户的互动、与客户的销售电话以及宏观经济活动。然后,我们使用这些特征来训练一个基本的 XGBoost 模型,以预测客户在其订阅到期时是否会续订
[1]:
# This cell defines the functions we use to generate the data in our scenario
import numpy as np
import pandas as pd
import scipy.stats
import sklearn
import xgboost
class FixableDataFrame(pd.DataFrame):
"""Helper class for manipulating generative models."""
def __init__(self, *args, fixed={}, **kwargs):
self.__dict__["__fixed_var_dictionary"] = fixed
super().__init__(*args, **kwargs)
def __setitem__(self, key, value):
out = super().__setitem__(key, value)
if isinstance(key, str) and key in self.__dict__["__fixed_var_dictionary"]:
out = super().__setitem__(key, self.__dict__["__fixed_var_dictionary"][key])
return out
# generate the data
def generator(n, fixed={}, seed=0):
"""The generative model for our subscriber retention example."""
if seed is not None:
np.random.seed(seed)
X = FixableDataFrame(fixed=fixed)
# the number of sales calls made to this customer
X["Sales calls"] = np.random.uniform(0, 4, size=(n,)).round()
# the number of sales calls made to this customer
X["Interactions"] = X["Sales calls"] + np.random.poisson(0.2, size=(n,))
# the health of the regional economy this customer is a part of
X["Economy"] = np.random.uniform(0, 1, size=(n,))
# the time since the last product upgrade when this customer came up for renewal
X["Last upgrade"] = np.random.uniform(0, 20, size=(n,))
# how much the user perceives that they need the product
X["Product need"] = X["Sales calls"] * 0.1 + np.random.normal(0, 1, size=(n,))
# the fractional discount offered to this customer upon renewal
X["Discount"] = ((1 - scipy.special.expit(X["Product need"])) * 0.5 + 0.5 * np.random.uniform(0, 1, size=(n,))) / 2
# What percent of the days in the last period was the user actively using the product
X["Monthly usage"] = scipy.special.expit(X["Product need"] * 0.3 + np.random.normal(0, 1, size=(n,)))
# how much ad money we spent per user targeted at this user (or a group this user is in)
X["Ad spend"] = (
X["Monthly usage"] * np.random.uniform(0.99, 0.9, size=(n,)) + (X["Last upgrade"] < 1) + (X["Last upgrade"] < 2)
)
# how many bugs did this user encounter in the since their last renewal
X["Bugs faced"] = np.array([np.random.poisson(v * 2) for v in X["Monthly usage"]])
# how many bugs did the user report?
X["Bugs reported"] = (X["Bugs faced"] * scipy.special.expit(X["Product need"])).round()
# did the user renew?
X["Did renew"] = scipy.special.expit(
7
* (
0.18 * X["Product need"]
+ 0.08 * X["Monthly usage"]
+ 0.1 * X["Economy"]
+ 0.05 * X["Discount"]
+ 0.05 * np.random.normal(0, 1, size=(n,))
+ 0.05 * (1 - X["Bugs faced"] / 20)
+ 0.005 * X["Sales calls"]
+ 0.015 * X["Interactions"]
+ 0.1 / (X["Last upgrade"] / 4 + 0.25)
+ X["Ad spend"] * 0.0
- 0.45
)
)
# in real life we would make a random draw to get either 0 or 1 for if the
# customer did or did not renew. but here we leave the label as the probability
# so that we can get less noise in our plots. Uncomment this line to get
# noiser causal effect lines but the same basic results
X["Did renew"] = scipy.stats.bernoulli.rvs(X["Did renew"])
return X
def user_retention_dataset():
"""The observed data for model training."""
n = 10000
X_full = generator(n)
y = X_full["Did renew"]
X = X_full.drop(["Did renew", "Product need", "Bugs faced"], axis=1)
return X, y
def fit_xgboost(X, y):
"""Train an XGBoost model with early stopping."""
X_train, X_test, y_train, y_test = sklearn.model_selection.train_test_split(X, y)
dtrain = xgboost.DMatrix(X_train, label=y_train)
dtest = xgboost.DMatrix(X_test, label=y_test)
model = xgboost.train(
{"eta": 0.001, "subsample": 0.5, "max_depth": 2, "objective": "reg:logistic"},
dtrain,
num_boost_round=200000,
evals=((dtest, "test"),),
early_stopping_rounds=20,
verbose_eval=False,
)
return model
[2]:
X, y = user_retention_dataset()
model = fit_xgboost(X, y)
一旦我们手头有了 XGBoost 客户留存模型,我们就可以开始使用像 SHAP 这样的可解释性工具来探索它学到了什么。我们首先绘制模型中每个特征的全局重要性
[3]:
import shap
explainer = shap.Explainer(model)
shap_values = explainer(X)
clust = shap.utils.hclust(X, y, linkage="single")
shap.plots.bar(shap_values, clustering=clust, clustering_cutoff=1)
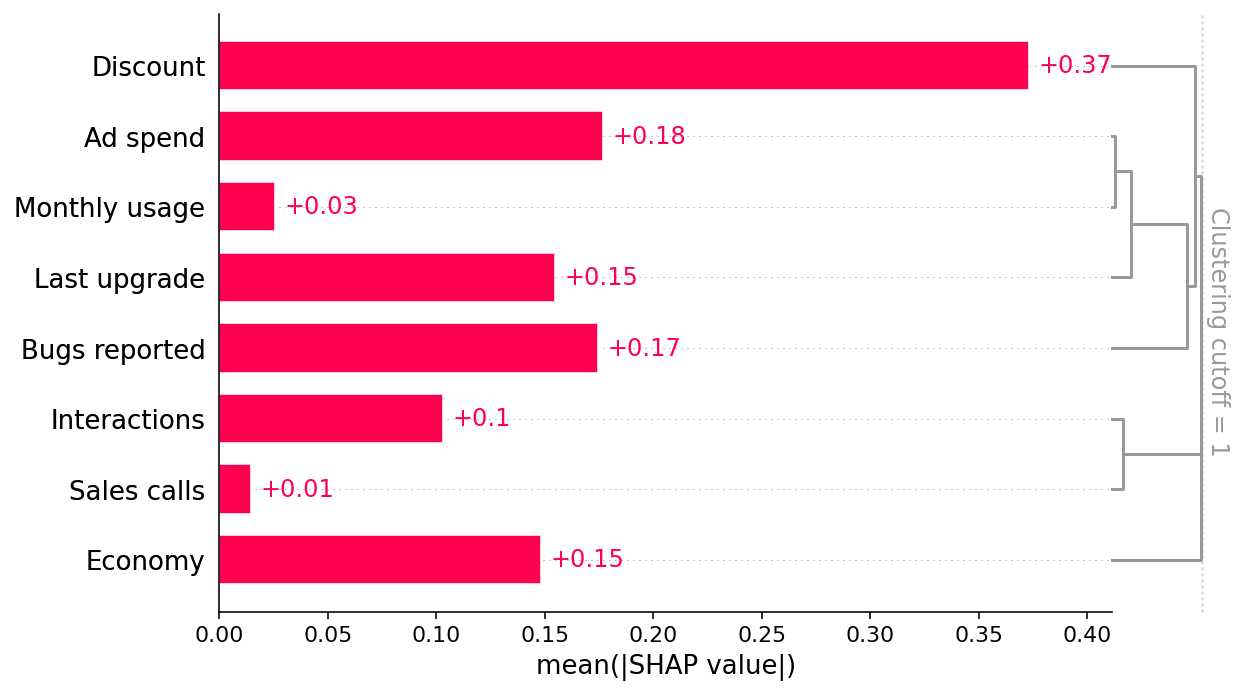
此条形图显示,提供的折扣、广告支出和报告的错误数量是驱动模型预测客户留存率的三个最主要因素。这很有趣,乍一看也很合理。条形图还包括特征冗余聚类,我们稍后将使用它。
然而,当我们深入挖掘并查看更改每个特征的值如何影响模型的预测时,我们发现了一些违反直觉的模式。SHAP 散点图显示了更改特征值如何影响模型对续订概率的预测。如果蓝点遵循递增模式,则意味着特征越大,模型预测的续订概率越高。
[4]:
shap.plots.scatter(shap_values, ylabel="SHAP value\n(higher means more likely to renew)")
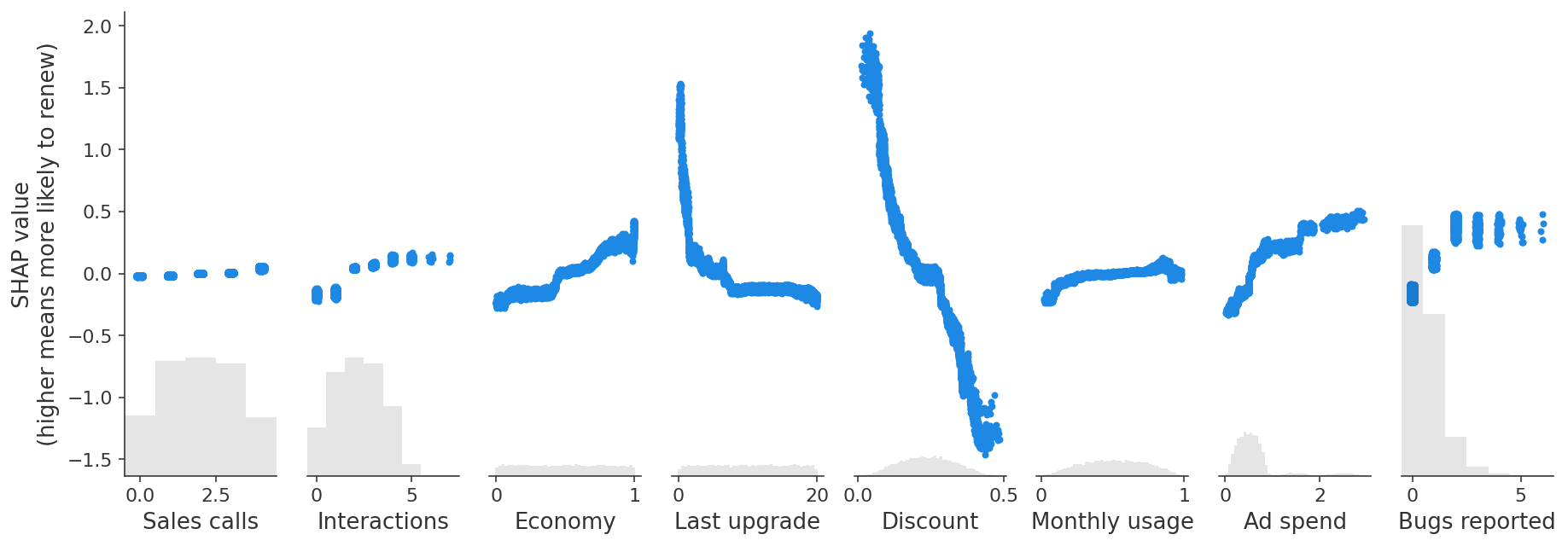
预测任务与因果任务
散点图显示了一些令人惊讶的发现: - 报告更多错误的用户更有可能续订! - 获得更大折扣的用户不太可能续订!
我们三次检查了我们的代码和数据管道,以排除错误,然后与一些业务合作伙伴交谈,他们提供了一个直观的解释: - 高度使用且重视产品的用户更有可能报告错误并续订其订阅。 - 销售人员倾向于向他们认为不太可能对产品感兴趣的客户提供高折扣,而这些客户的流失率更高。
模型中这些起初违反直觉的关系是一个问题吗?这取决于我们的目标是什么!
我们这个模型的最初目标是预测客户留存率,这对于诸如估算财务规划的未来收入之类的项目很有用。由于报告更多错误的用户实际上更有可能续订,因此在模型中捕捉这种关系有助于预测。只要我们的模型具有良好的样本外拟合度,我们就应该能够为财务部门提供良好的预测,因此不必担心模型中这种关系的方向。
这是一个被称为 预测任务 的任务类别的示例。在预测任务中,目标是根据一组特征 X 预测结果 Y(例如续订)。预测练习的关键组成部分是我们只关心预测 model(X) 在类似于我们训练集的数据分布中接近 Y。 X 和 Y 之间的简单相关性对于这些类型的预测可能很有帮助。
但是,假设第二个团队使用我们的预测模型,其新目标是确定我们公司可以采取哪些行动来留住更多客户。这个团队非常关心每个 X 特征如何与 Y 相关,不仅在我们训练分布中,而且在世界发生变化时产生的反事实情景中。在这种用例中,仅仅识别变量之间稳定的相关性是不够的;这个团队想知道操纵特征 X 是否会导致 Y 发生变化。想象一下,当您告诉工程主管您希望他引入新的错误以增加客户续订量时,他的表情会是什么样!
这是一个被称为 因果任务 的任务类别的示例。在因果任务中,我们想知道改变世界的某个方面 X(例如报告的错误)如何影响结果 Y(续订)。在这种情况下,至关重要的是要知道改变 X 是否会导致 Y 增加,或者数据中的关系是否仅仅是相关性的。
估计因果效应的挑战
理解因果关系的一个有用工具是写下我们感兴趣的数据生成过程的因果图。我们示例的因果图说明了为什么我们的 XGBoost 客户留存模型捕获的稳健预测关系与想要计划干预以提高留存率的团队感兴趣的因果关系不同。此图只是真实数据生成机制的摘要(如上定义)。实心椭圆形表示我们观察到的特征,而虚线椭圆形表示我们未测量的隐藏特征。每个特征都是指向它的所有特征的函数,加上一些随机效应。
在我们的示例中,我们知道因果图,因为我们模拟了数据。在实践中,真正的因果图是未知的,但我们或许可以使用特定于上下文的领域知识来推断哪些关系可能存在或不可能存在。
[5]:
import graphviz
names = [
"Bugs reported",
"Monthly usage",
"Sales calls",
"Economy",
"Discount",
"Last upgrade",
"Ad spend",
"Interactions",
]
g = graphviz.Digraph()
for name in names:
g.node(name, fontsize="10")
g.node("Product need", style="dashed", fontsize="10")
g.node("Bugs faced", style="dashed", fontsize="10")
g.node("Did renew", style="filled", fontsize="10")
g.edge("Product need", "Did renew")
g.edge("Product need", "Discount")
g.edge("Product need", "Bugs reported")
g.edge("Product need", "Monthly usage")
g.edge("Discount", "Did renew")
g.edge("Monthly usage", "Bugs faced")
g.edge("Monthly usage", "Did renew")
g.edge("Monthly usage", "Ad spend")
g.edge("Economy", "Did renew")
g.edge("Sales calls", "Did renew")
g.edge("Sales calls", "Product need")
g.edge("Sales calls", "Interactions")
g.edge("Interactions", "Did renew")
g.edge("Bugs faced", "Did renew")
g.edge("Bugs faced", "Bugs reported")
g.edge("Last upgrade", "Did renew")
g.edge("Last upgrade", "Ad spend")
g
[5]:
此图中有很多关系,但第一个重要的关注点是,我们能够测量的一些特征受到未测量的混淆特征(如产品需求和遇到的错误)的影响。例如,报告更多错误的用户遇到更多错误是因为他们更多地使用该产品,并且他们更有可能报告这些错误,因为他们更需要该产品。产品需求本身对续订具有直接的因果效应。由于我们无法直接衡量产品需求,因此我们在预测模型中最终捕获的报告错误和续订之间的相关性结合了遇到的错误的一个小的负面直接效应和来自产品需求的一个大的正面混淆效应。下图绘制了我们示例中的 SHAP 值与每个特征的真实因果效应(在本示例中已知,因为我们生成了数据)。
[6]:
def marginal_effects(generative_model, num_samples=100, columns=None, max_points=20, logit=True, seed=0):
"""Helper function to compute the true marginal causal effects."""
X = generative_model(num_samples)
if columns is None:
columns = X.columns
ys = [[] for _ in columns]
xs = [X[c].values for c in columns]
xs = np.sort(xs, axis=1)
xs = [xs[i] for i in range(len(xs))]
for i, c in enumerate(columns):
xs[i] = np.unique([np.nanpercentile(xs[i], v, method="nearest") for v in np.linspace(0, 100, max_points)])
for x in xs[i]:
Xnew = generative_model(num_samples, fixed={c: x}, seed=seed)
val = Xnew["Did renew"].mean()
if logit:
val = scipy.special.logit(val)
ys[i].append(val)
ys[i] = np.array(ys[i])
ys = [ys[i] - ys[i].mean() for i in range(len(ys))]
return list(zip(xs, ys))
shap.plots.scatter(
shap_values,
ylabel="SHAP value\n(higher means more likely to renew)",
overlay={"True causal effects": marginal_effects(generator, 10000, X.columns)},
)
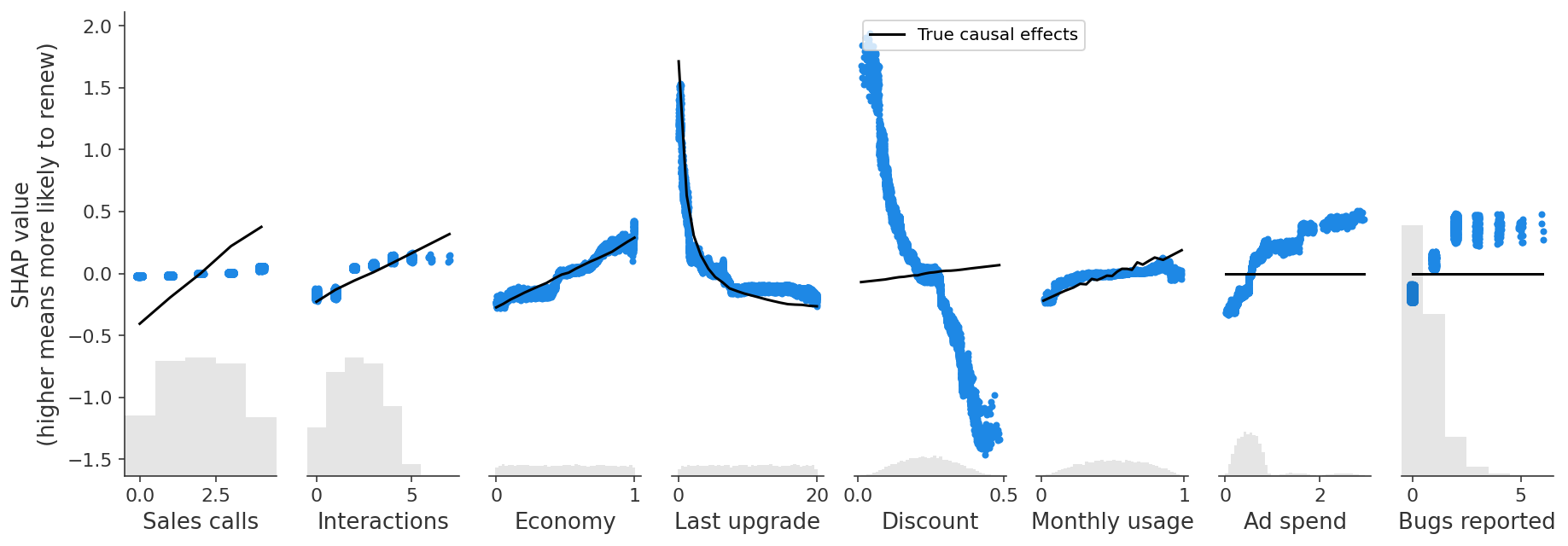
预测模型捕获了报告错误对留存率的总体积极影响(如 SHAP 所示),即使报告错误的因果效应为零,而遇到错误的效应为负。
我们在折扣方面看到了类似的问题,折扣也受未观察到的客户产品需求驱动。我们的预测模型发现折扣与留存率之间存在负相关关系,这是由与未观察到的特征“产品需求”的相关性驱动的,即使实际上折扣对续订具有小的正因果效应!换句话说,如果两个客户具有相同的产品需求并且在其他方面相似,那么折扣较大的客户更有可能续订。
当我们开始将预测模型解释为因果模型时,此图还揭示了第二个更隐蔽的问题。请注意,广告支出也存在类似的问题——它对留存率没有因果效应(黑线是平的),但预测模型正在捕捉积极效应!
在这种情况下,广告支出仅受上次升级和每月使用量的驱动,因此我们没有未观察到的混淆问题,而是有观察到的混淆问题。广告支出和影响广告支出的特征之间存在统计冗余。当我们有多个特征捕获的相同信息时,预测模型可以使用这些特征中的任何一个进行预测,即使它们并非都具有因果关系。虽然广告支出本身对续订没有因果效应,但它与驱动续订的几个特征密切相关。我们的正则化模型将广告支出识别为有用的预测指标,因为它总结了多个因果驱动因素(从而导致更稀疏的模型),但如果我们开始将其解释为因果效应,那将变得非常具有误导性。
我们现在将依次解决我们示例的每个部分,以说明预测模型何时可以准确衡量因果效应,以及何时不能。我们还将介绍一些因果工具,这些工具有时可以在预测模型失败的情况下估计因果效应。
预测模型何时可以回答因果问题
让我们从我们示例中的成功之处开始。请注意,我们的预测模型在捕获经济特征的真实因果效应方面做得很好(经济状况良好对留存率有积极影响)。那么,我们何时可以期望预测模型捕获真实的因果效应呢?
XGBoost 能够很好地估计经济的因果效应的重要因素是该特征的强大独立成分(在此模拟中);它对留存率的预测能力与其他任何测量的特征或任何未测量的混淆因素都没有很强的冗余性。因此,它不受未测量的混淆因素或特征冗余的偏差的影响。
[7]:
# Economy is independent of other measured features.
shap.plots.bar(shap_values, clustering=clust, clustering_cutoff=1)
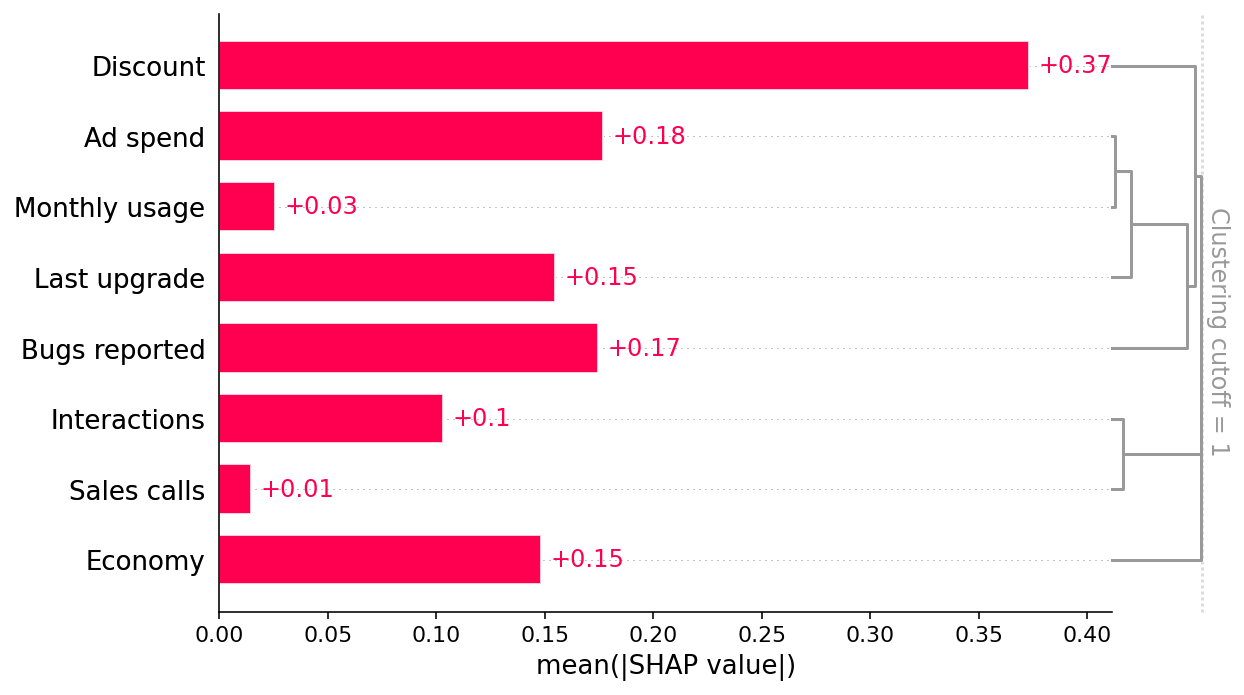
由于我们已将聚类添加到 SHAP 条形图的右侧,因此我们可以将数据的冗余结构视为树状图。当特征在树状图的底部(左侧)合并在一起时,这意味着这些特征包含的关于结果(续订)的信息非常冗余,并且模型可以使用任一特征。当特征在树状图的顶部(右侧)合并在一起时,这意味着它们包含的关于结果的信息彼此独立。
我们可以看到,经济与所有其他测量的特征都是独立的,方法是注意经济在聚类树状图的最顶部之前没有与其他任何特征合并。这告诉我们,经济不受观察到的混淆因素的影响。但是,要相信经济效应是因果关系,我们还需要检查未观察到的混淆因素。检查未测量的混淆因素更难,需要使用领域知识(在上面的示例中由业务合作伙伴提供)。
对于经典的预测性机器学习模型要提供因果结果,特征不仅需要与其他模型中的特征独立,还需要与未观察到的混淆因素独立。自然地找到表现出这种独立性水平的感兴趣的驱动因素并不常见,但是当我们的数据包含一些实验时,我们通常可以找到独立特征的示例。
预测模型何时无法回答因果问题,但因果推断方法可以提供帮助
在大多数真实世界的数据集中,特征不是独立的且未消除混淆的,因此标准预测模型将无法学习到真实的因果效应。因此,用 SHAP 解释它们不会揭示因果效应。但并非一切都失去了,有时我们可以使用观察性因果推断工具来修复或至少最大程度地减少此问题。
观察到的混淆因素
因果推断可以提供帮助的第一种情况是观察到的混淆因素。当存在另一个特征,该特征因果地影响原始特征和我们正在预测的结果时,该特征是“混淆的”。如果我们能够测量该其他特征,则称其为观察到的混淆因素。
[8]:
# Ad spend is very redundant with Monthly usage and Last upgrade.
shap.plots.bar(shap_values, clustering=clust, clustering_cutoff=1)
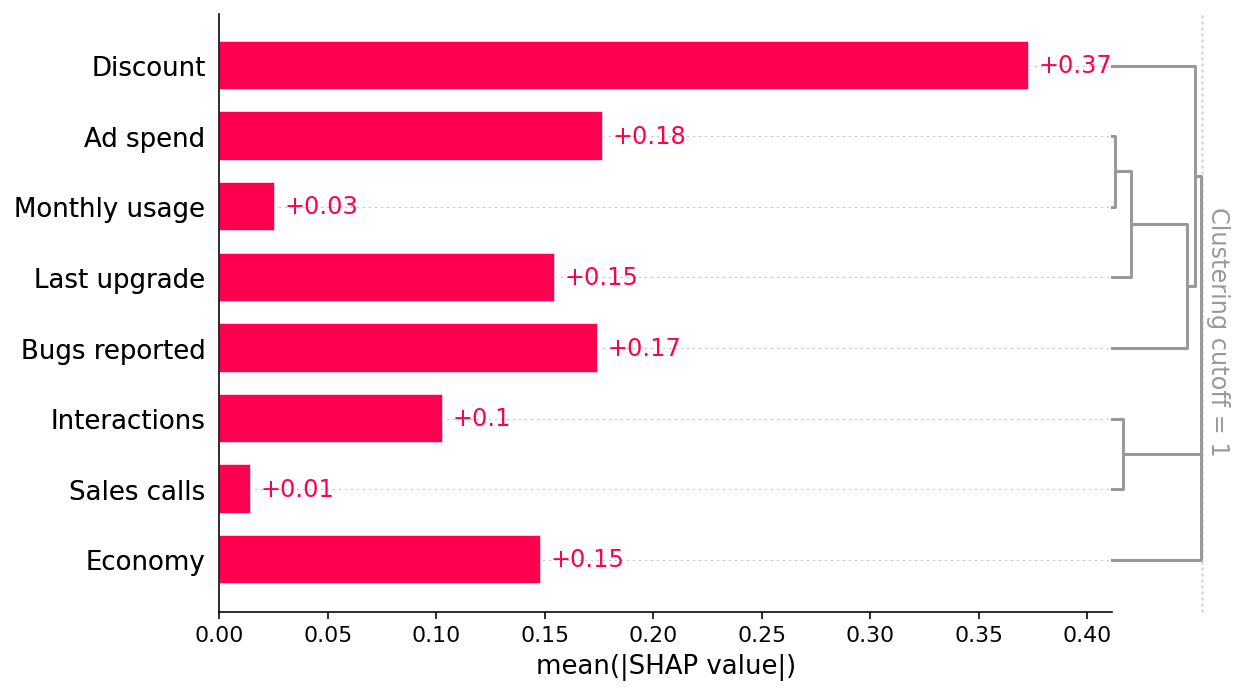
我们场景中的一个示例是广告支出特征。即使广告支出对留存率没有直接的因果效应,但它与上次升级和每月使用量特征相关,而这些特征确实驱动了留存率。我们的预测模型将广告支出识别为留存率的最佳单一预测指标之一,因为它通过相关性捕获了如此多的真实因果驱动因素。XGBoost 施加了正则化,这是一种花哨的说法,它试图选择仍然可以很好地预测的最简单模型。如果它可以使用一个特征而不是三个特征来同样好地进行预测,它将倾向于这样做以避免过拟合。但这意味着,如果广告支出与上次升级和每月使用量高度相关,则 XGBoost 可能会使用广告支出而不是因果特征!XGBoost(或任何其他具有正则化的机器学习模型)的此属性对于生成对未来留存率的稳健预测非常有用,但对于理解如果我们想提高留存率应该操纵哪些特征则不利。
这突出了将正确的建模工具与每个问题相匹配的重要性。与错误报告示例不同,认为增加广告支出会增加留存率的结论在直觉上没有错。如果不适当关注我们的预测模型正在测量什么和没有测量什么,我们很容易继续进行此发现,并且只有在增加广告支出而没有获得我们预期的续订结果后才意识到我们的错误。
观察性因果推断
关于广告支出的好消息是,我们可以测量所有可能混淆它的特征(那些在上面的因果图中箭头指向广告支出的特征)。因此,这是一个观察到的混淆因素的示例,我们应该能够仅使用我们已经收集的数据来解开相关性模式;我们只需要使用来自观察性因果推断的正确工具。这些工具允许我们指定哪些特征可能混淆广告支出,然后调整这些特征,以获得广告支出对产品续订的因果效应的未消除混淆的估计。
双重/去偏机器学习是一种特别灵活的观察性因果推断工具。它使用您想要的任何机器学习模型首先消除感兴趣特征(即广告支出)的混淆,然后估计更改该特征的平均因果效应(即因果效应的平均斜率)。
双重 ML 的工作原理如下: 1. 训练一个模型,使用一组可能的混淆因素(即任何不是由广告支出引起的特征)来预测感兴趣的特征(即广告支出)。 2. 训练一个模型,使用同一组可能的混淆因素来预测结果(即是否续订)。 3. 训练一个模型,使用感兴趣的因果特征的残差变异来预测结果的残差变异(减去我们的预测后剩下的变异)。
直觉是,如果广告支出导致续订,那么无法通过其他混淆特征预测的广告支出部分应与无法通过其他混淆特征预测的续订部分相关。换句话说,双重 ML 假设存在一个独立的(未观察到的)噪声特征,该特征会影响广告支出(因为广告支出并非完全由其他特征决定),因此我们可以推断此独立噪声特征的值,然后在该独立特征上训练模型以预测输出。
虽然我们可以手动完成所有双重 ML 步骤,但使用像 econML 或 CausalML 这样的因果推断包更容易。在这里,我们使用 econML 的 LinearDML 模型。这返回一个 P 值,指示该处理是否具有非零因果效应,并且在我们的场景中效果非常好,正确地识别出没有证据表明广告支出对续订有因果效应(P 值 = 0.85)
[9]:
import matplotlib.pyplot as plt
from econml.dml import LinearDML
from sklearn.base import BaseEstimator, clone
class RegressionWrapper(BaseEstimator):
"""Turns a classifier into a 'regressor'.
We use the regression formulation of double ML, so we need to approximate the classifer
as a regression model. This treats the probabilities as just quantitative value targets
for least squares regression, but it turns out to be a reasonable approximation.
"""
def __init__(self, clf):
self.clf = clf
def fit(self, X, y, **kwargs):
self.clf_ = clone(self.clf)
self.clf_.fit(X, y, **kwargs)
return self
def predict(self, X):
return self.clf_.predict_proba(X)[:, 1]
# Run Double ML, controlling for all the other features
def double_ml(y, causal_feature, control_features):
"""Use doubleML from econML to estimate the slope of the causal effect of a feature."""
xgb_model = xgboost.XGBClassifier(objective="binary:logistic", random_state=42)
est = LinearDML(model_y=RegressionWrapper(xgb_model))
est.fit(y, causal_feature, W=control_features)
return est.effect_inference()
def plot_effect(effect, xs, true_ys, ylim=None):
"""Plot a double ML effect estimate from econML as a line.
Note that the effect estimate from double ML is an average effect *slope* not a full
function. So we arbitrarily draw the slope of the line as passing through the origin.
"""
plt.figure(figsize=(5, 3))
pred_xs = [xs.min(), xs.max()]
mid = (xs.min() + xs.max()) / 2
[effect.pred[0] * (xs.min() - mid), effect.pred[0] * (xs.max() - mid)]
plt.plot(xs, true_ys - true_ys[0], label="True causal effect", color="black", linewidth=3)
point_pred = effect.point_estimate * pred_xs
pred_stderr = effect.stderr * np.abs(pred_xs)
plt.plot(
pred_xs,
point_pred - point_pred[0],
label="Double ML slope",
color=shap.plots.colors.blue_rgb,
linewidth=3,
)
# 99.9% CI
plt.fill_between(
pred_xs,
point_pred - point_pred[0] - 3.291 * pred_stderr,
point_pred - point_pred[0] + 3.291 * pred_stderr,
alpha=0.2,
color=shap.plots.colors.blue_rgb,
)
plt.legend()
plt.xlabel("Ad spend", fontsize=13)
plt.ylabel("Zero centered effect")
if ylim is not None:
plt.ylim(*ylim)
plt.gca().xaxis.set_ticks_position("bottom")
plt.gca().yaxis.set_ticks_position("left")
plt.gca().spines["right"].set_visible(False)
plt.gca().spines["top"].set_visible(False)
plt.show()
# estimate the causal effect of Ad spend controlling for all the other features
causal_feature = "Ad spend"
control_features = [
"Sales calls",
"Interactions",
"Economy",
"Last upgrade",
"Discount",
"Monthly usage",
"Bugs reported",
]
effect = double_ml(y, X[causal_feature], X.loc[:, control_features])
# plot the estimated slope against the true effect
xs, true_ys = marginal_effects(generator, 10000, X[["Ad spend"]], logit=False)[0]
plot_effect(effect, xs, true_ys, ylim=(-0.2, 0.2))
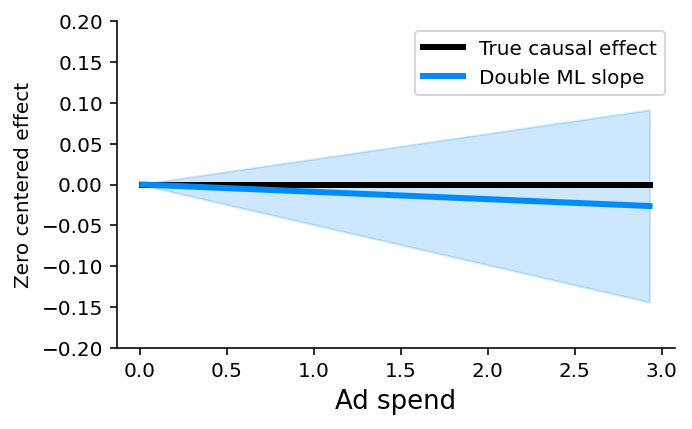
请记住,双重 ML(或任何其他观察性因果推断方法)仅当您可以测量和识别您想要估计因果效应的特征的所有可能的混淆因素时才有效。在这里,我们知道因果图,并且可以看到每月使用量和上次升级是我们需要控制的两个直接混淆因素。但是,如果我们不知道因果图,我们仍然可以查看 SHAP 条形图中的冗余,并看到每月使用量和上次升级是最冗余的特征,因此是很好的控制候选者(折扣和报告的错误也是如此)。
非混淆冗余
因果推断可以提供帮助的第二种情况是非混淆冗余。当我们要为其寻找因果效应的特征因果地驱动或被模型中包含的另一个特征驱动时,就会发生这种情况,但该其他特征不是我们感兴趣的特征的混淆因素。
[10]:
# Interactions and sales calls are very redundant with one another.
shap.plots.bar(shap_values, clustering=clust, clustering_cutoff=1)
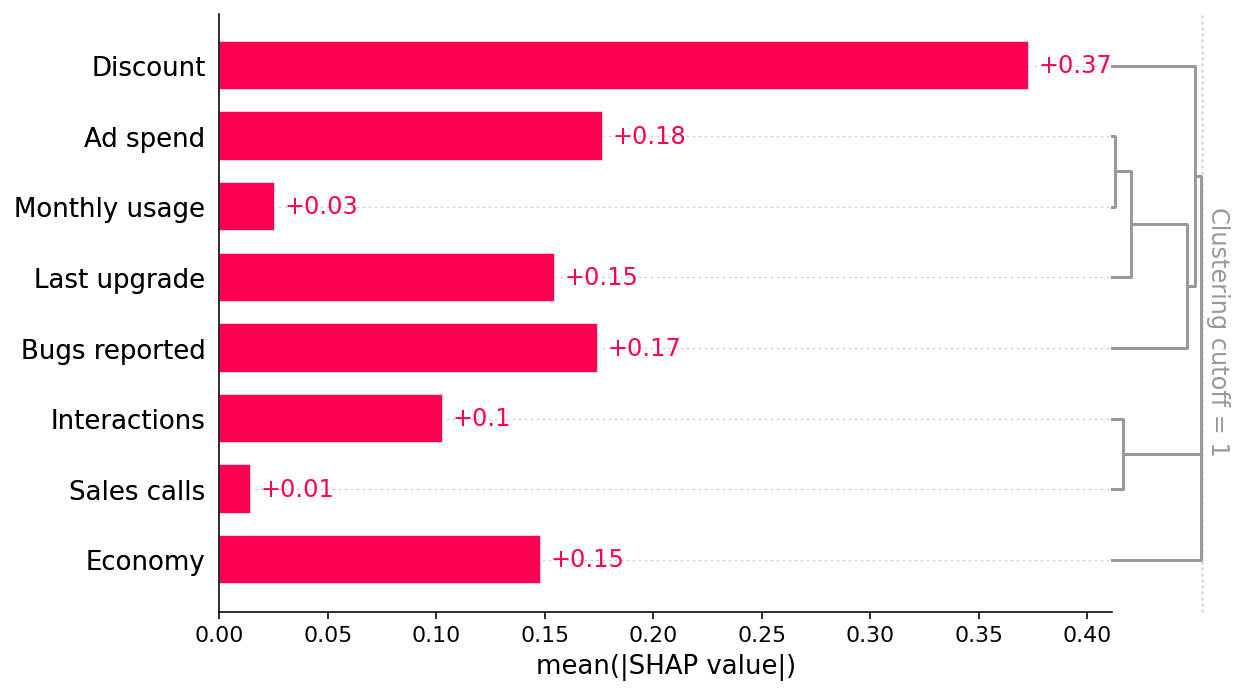
这方面的一个例子是销售电话特征。销售电话直接影响留存率,但也通过互动对留存率产生间接影响。当我们在模型中同时包含互动和销售电话特征时,这两个特征共享的因果效应被迫在它们之间分散。我们可以在上面的 SHAP 散点图中看到这一点,该图显示了 XGBoost 如何低估销售电话的真实因果效应,因为大部分效应都放在了互动特征上。
原则上,可以通过从模型中删除冗余变量来修复非混淆冗余(见下文)。例如,如果我们从模型中删除互动,那么我们将捕获进行销售电话对续订概率的全部影响。这种删除对于双重 ML 也很重要,因为如果您控制了由感兴趣的特征引起的下游特征,则双重 ML 将无法捕获间接因果效应。在这种情况下,双重 ML 将仅衡量不通过其他特征的“直接”效应。但是,双重 ML 对于控制上游非混淆冗余(其中冗余特征导致感兴趣的特征)是稳健的,尽管这将降低您检测真实效应的统计功效。
不幸的是,我们通常不知道真正的因果图,因此很难知道另一个特征何时因观察到的混淆与非混淆冗余而与我们感兴趣的特征冗余。如果是由于混淆,那么我们应该使用像双重 ML 这样的方法来控制该特征,而如果是下游结果,那么如果我们想要完整的因果效应而不是仅直接效应,我们应该从模型中删除该特征。控制我们不应该控制的特征往往会隐藏或分散因果效应,而未能控制我们应该控制的特征往往会推断出不存在的因果效应。当您不确定时,通常控制特征是更安全的选择。
[11]:
# Fit, explain, and plot a univariate model with just Sales calls
# Note how this model does not have to split of credit between Sales calls and
# Interactions, so we get a better agreement with the true causal effect.
sales_calls_model = fit_xgboost(X[["Sales calls"]], y)
sales_calls_shap_values = shap.Explainer(sales_calls_model)(X[["Sales calls"]])
shap.plots.scatter(
sales_calls_shap_values,
overlay={"True causal effects": marginal_effects(generator, 10000, ["Sales calls"])},
)
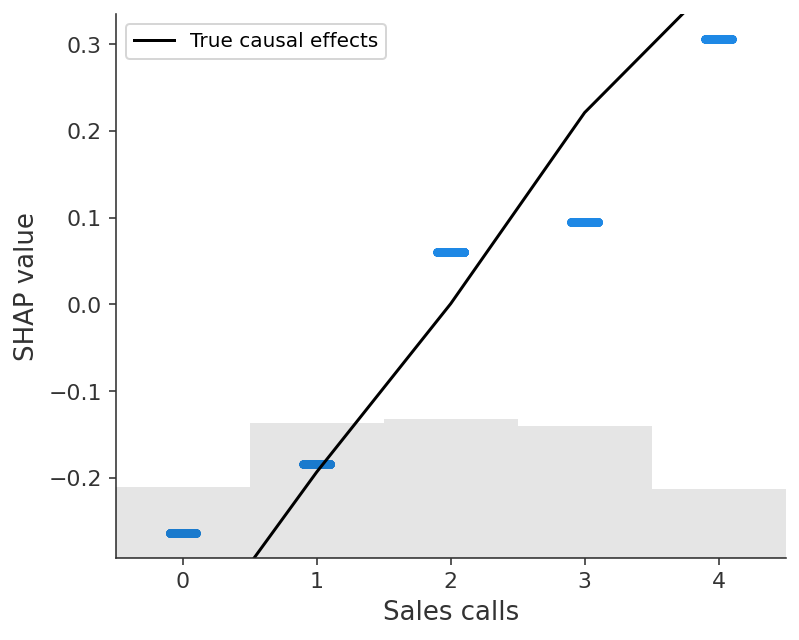
当预测模型和消除混淆的方法都无法回答因果问题时
双重 ML(或任何其他假设未消除混淆的因果推断方法)仅当您可以测量和识别您想要估计因果效应的特征的所有可能的混淆因素时才有效。如果您无法测量所有混淆因素,那么您就处于最困难的情况下:未观察到的混淆因素。
[12]:
# Discount and Bugs reported seem are fairly independent of the other features we can
# measure, but they are not independent of Product need, which is an unobserved confounder.
shap.plots.bar(shap_values, clustering=clust, clustering_cutoff=1)
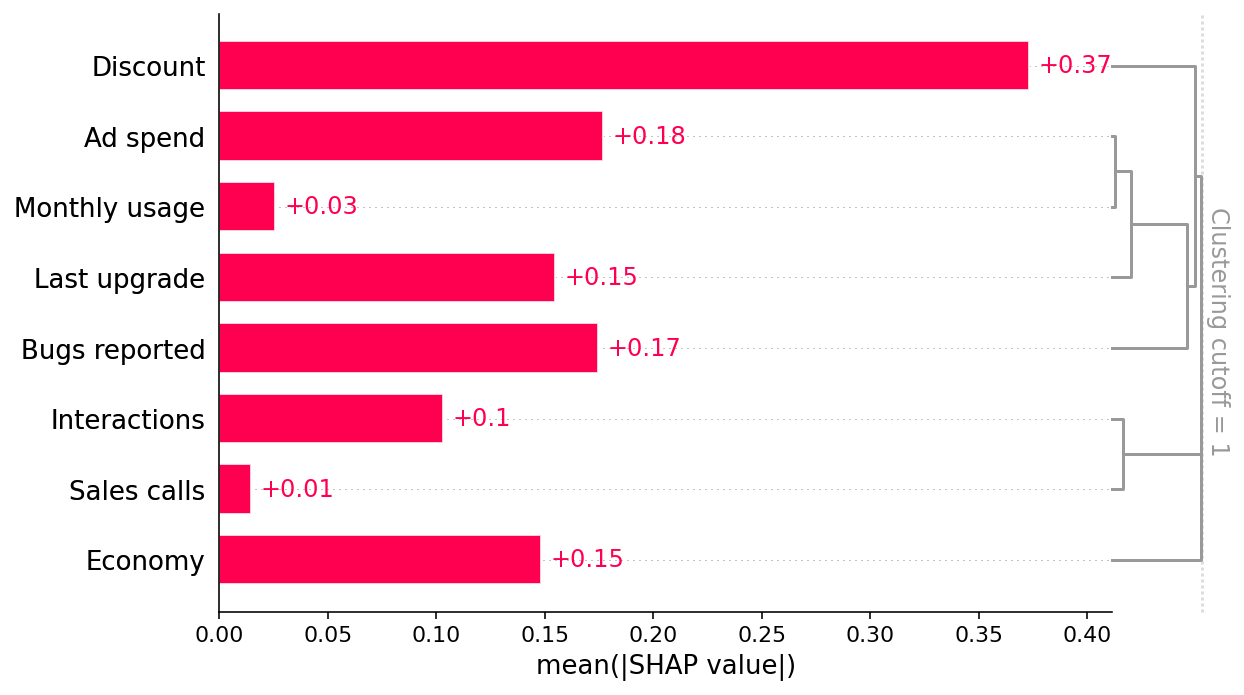
折扣和报告的错误特征都受到未观察到的混淆因素的影响,因为并非所有重要变量(例如,产品需求和遇到的错误)都在数据中测量。即使这两个特征都相对独立于模型中的所有其他特征,但也存在重要的驱动因素未被测量。在这种情况下,预测模型和需要观察混淆因素的因果模型(如双重 ML)都会失败。这就是为什么双重 ML 为折扣特征估计了一个大的负因果效应,即使在控制了所有其他观察到的特征之后也是如此
[13]:
# estimate the causal effect of Ad spend controlling for all the other features
causal_feature = "Discount"
control_features = [
"Sales calls",
"Interactions",
"Economy",
"Last upgrade",
"Monthly usage",
"Ad spend",
"Bugs reported",
]
effect = double_ml(y, X[causal_feature], X.loc[:, control_features])
# plot the estimated slope against the true effect
xs, true_ys = marginal_effects(generator, 10000, X[[causal_feature]], logit=False)[0]
plot_effect(effect, xs, true_ys, ylim=(-0.5, 0.2))
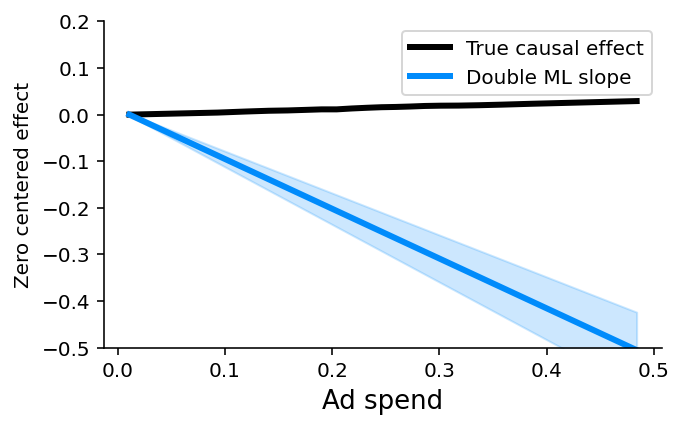
除非能够测量以前未测量的特征(或与它们相关的特征),否则在存在未观察到的混淆因素的情况下找到因果效应是很困难的。在这些情况下,识别可以为政策提供信息的因果效应的唯一方法是创建或利用某种随机化,以打破感兴趣的特征与未测量的混淆因素之间的相关性。随机实验仍然是在这种情况下寻找因果效应的黄金标准。
基于工具变量、差异中差异或回归不连续性原理的专门因果工具有时可以利用部分随机化,即使在完全实验不可能的情况下也是如此。例如,工具变量技术可用于识别在无法随机分配治疗的情况下的因果效应,但我们可以随机地引导一些客户接受治疗,例如发送电子邮件鼓励他们探索新的产品功能。当新疗法的引入在不同群体中错开时,差异中差异方法可能很有帮助。最后,当治疗模式表现出明显的临界值时(例如,根据特定的、可测量的特征(如每月收入超过 5,000 美元)获得治疗资格),回归不连续性方法是一个不错的选择。
总结
像 XGBoost 或 LightGBM 这样的灵活预测模型是解决预测问题的强大工具。但是,它们本质上不是因果模型,因此在许多常见情况下,使用 SHAP 解释它们将无法准确回答因果问题。除非模型中的特征是实验变异的结果,否则在不考虑混淆因素的情况下将 SHAP 应用于预测模型通常不是衡量用于为政策提供信息的因果影响的合适工具。SHAP 和其他可解释性工具对于因果推断可能很有用,并且 SHAP 已集成到许多因果推断包中,但这些用例本质上是明确的因果关系。为此,使用我们为预测问题收集的相同数据,并使用特别设计用于返回因果效应的因果推断方法(如双重 ML)通常是为政策提供信息的良好方法。在其他情况下,只有实验或其他随机化来源才能真正回答“如果...会怎样”的问题。因果推断始终要求我们做出重要的假设。本文的主要观点是,我们将普通预测模型解释为因果模型所做的假设通常是不现实的。