使用 Keras 进行人口普查收入分类

要下载此 notebook 的副本，请访问 github。

此 notebook 展示了如何使用核解释器（kernel explainer）和联盟解释器（coalition explainer）来解释神经网络。

[1]:

import matplotlib.pyplot as plt
from keras.layers import Dense, Dropout, Embedding, Flatten, Input, concatenate
from keras.models import Model
from sklearn.model_selection import train_test_split

import shap

# print the JS visualization code to the notebook
shap.initjs()

c:\programming\shap\.venv\lib\site-packages\tqdm\auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm

加载数据集

[2]:

X, y = shap.datasets.adult()
X_display, y_display = shap.datasets.adult(display=True)

# normalize data (this is important for model convergence)
dtypes = list(zip(X.dtypes.index, map(str, X.dtypes)))
for k, dtype in dtypes:
    if dtype == "float32":
        X[k] -= X[k].mean()
        X[k] /= X[k].std()

X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.2, random_state=7)

训练 Keras 模型

[3]:

# build model
input_els = []
encoded_els = []
for k, dtype in dtypes:
    input_els.append(Input(shape=(1,)))
    if dtype == "int8":
        e = Flatten()(Embedding(X_train[k].max() + 1, 1)(input_els[-1]))
    else:
        e = input_els[-1]
    encoded_els.append(e)
encoded_els = concatenate(encoded_els)
layer1 = Dropout(0.5)(Dense(100, activation="relu")(encoded_els))
out = Dense(1)(layer1)

# train model
regression = Model(inputs=input_els, outputs=[out])
regression.compile(optimizer="adam", loss="binary_crossentropy")
regression.fit(
    [X_train[k].values for k, t in dtypes],
    y_train,
    epochs=50,
    batch_size=512,
    shuffle=True,
    validation_data=([X_valid[k].values for k, t in dtypes], y_valid),
)

Epoch 1/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 3s 14ms/step - loss: 3.1297 - val_loss: 0.8234
Epoch 2/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - loss: 1.9760 - val_loss: 1.0105
Epoch 3/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.6813 - val_loss: 0.5041
Epoch 4/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.5226 - val_loss: 0.5412
Epoch 5/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.4729 - val_loss: 0.8485
Epoch 6/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.5344 - val_loss: 0.4860
Epoch 7/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.3546 - val_loss: 0.4602
Epoch 8/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.2509 - val_loss: 0.4429
Epoch 9/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.2643 - val_loss: 0.4513
Epoch 10/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.1453 - val_loss: 0.4645
Epoch 11/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.1067 - val_loss: 0.4369
Epoch 12/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.1187 - val_loss: 0.4549
Epoch 13/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.0626 - val_loss: 0.4600
Epoch 14/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 1.0424 - val_loss: 0.4231
Epoch 15/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 0.9474 - val_loss: 0.4182
Epoch 16/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 0.8717 - val_loss: 0.4932
Epoch 17/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 3ms/step - loss: 0.9838 - val_loss: 0.4509
Epoch 18/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.8657 - val_loss: 0.4175
Epoch 19/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.9054 - val_loss: 0.4238
Epoch 20/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.8049 - val_loss: 0.4411
Epoch 21/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.7607 - val_loss: 0.4126
Epoch 22/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.6943 - val_loss: 0.4062
Epoch 23/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.6739 - val_loss: 0.4163
Epoch 24/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.6874 - val_loss: 0.3914
Epoch 25/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.6113 - val_loss: 0.3714
Epoch 26/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.5662 - val_loss: 0.3684
Epoch 27/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 8ms/step - loss: 0.6947 - val_loss: 0.6365
Epoch 28/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.8330 - val_loss: 0.4122
Epoch 29/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.6455 - val_loss: 0.4116
Epoch 30/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 1s 10ms/step - loss: 0.5741 - val_loss: 0.3864
Epoch 31/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.6159 - val_loss: 0.3896
Epoch 32/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.5781 - val_loss: 0.3807
Epoch 33/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 0.5281 - val_loss: 0.3799
Epoch 34/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.5337 - val_loss: 0.3780
Epoch 35/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.5242 - val_loss: 0.3794
Epoch 36/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.5320 - val_loss: 0.3818
Epoch 37/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.5084 - val_loss: 0.3808
Epoch 38/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.4883 - val_loss: 0.3776
Epoch 39/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.4777 - val_loss: 0.3728
Epoch 40/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.4945 - val_loss: 0.3745
Epoch 41/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.4776 - val_loss: 0.3721
Epoch 42/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.4781 - val_loss: 0.3694
Epoch 43/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.4621 - val_loss: 0.3690
Epoch 44/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 7ms/step - loss: 0.4481 - val_loss: 0.3721
Epoch 45/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.4557 - val_loss: 0.3688
Epoch 46/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.4404 - val_loss: 0.3702
Epoch 47/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.4545 - val_loss: 0.3753
Epoch 48/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - loss: 0.4627 - val_loss: 0.3737
Epoch 49/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.4358 - val_loss: 0.3740
Epoch 50/50
51/51 ━━━━━━━━━━━━━━━━━━━━ 0s 4ms/step - loss: 0.4449 - val_loss: 0.3745

[3]:

<keras.src.callbacks.history.History at 0x2b1bf5beb30>

解释预测

在这里，我们使用上面训练好的 Keras 模型，并解释为什么它对不同个体做出不同的预测。SHAP 要求模型函数接受一个二维 numpy 数组作为输入，因此我们围绕原始的 Keras 预测函数定义一个包装函数。

[4]:

def f(X):
    return regression.predict([X[:, i] for i in range(X.shape[1])]).flatten()

解释单个预测

在这里，我们从数据集中选取 50 个样本来代表“典型”的特征值，然后使用 500 个扰动样本来估算给定预测的 SHAP 值。请注意，这需要对模型进行 500 * 50 次评估。

[5]:

X.iloc[299, :]

[5]:

Age               -0.042641
Workclass          4.000000
Education-Num     -0.420053
Marital Status     0.000000
Occupation        12.000000
Relationship       0.000000
Race               4.000000
Sex                1.000000
Capital Gain      -0.145918
Capital Loss      -0.216656
Hours per week     3.204112
Country           39.000000
Name: 299, dtype: float64

[6]:

X.iloc[299:300, :]

[6]:

	年龄	工作类别	受教育年限	婚姻状况	职业	关系	种族	性别	资本收益	资本损失	每周工作小时数	国家
299	-0.042641	4	-0.420053	0	12	0	4	1	-0.145918	-0.216656	3.204112	39

[7]:

import numpy as np

f(np.array(X.iloc[299:300, :]))

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 244ms/step

[7]:

array([0.23898253], dtype=float32)

[8]:

kernel_explainer = shap.KernelExplainer(f, X.iloc[:50, :])
shap_values = kernel_explainer.shap_values(X.iloc[299, :], nsamples=500)

shap.force_plot(kernel_explainer.expected_value, shap_values, X_display.iloc[299, :])

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 63ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 3s 3ms/step

[8]:

可视化已省略，Javascript 库未加载！
你是否已在此 notebook 中运行 `initjs()`？如果此 notebook 来自其他用户，你还必须信任此 notebook (文件 -> 信任 notebook)。如果你在 github 上查看此 notebook，则 Javascript 已为安全起见被剥离。如果你正在使用 JupyterLab，此错误是因为尚未编写 JupyterLab 扩展。

[9]:

shap_values = kernel_explainer(X.iloc[299:300, :])

  0%|          | 0/1 [00:00<?, ?it/s]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 257ms/step
3238/3238 ━━━━━━━━━━━━━━━━━━━━ 6s 2ms/step

100%|██████████| 1/1 [00:07<00:00,  7.74s/it]

设置联盟解释器 (Coalition Explainer)。

[10]:

partition_tree = {
    "cluster_16": {
        "cluster_12": {
            "cluster_8": {"Age": "Age", "Workclass": "Workclass"},
            "cluster_9": {
                "Education-Num": "Education-Num",
                "Marital Status": "Marital Status",
            },
        },
        "cluster_13": {
            "cluster_10": {"Occupation": "Occupation", "Relationship": "Relationship"},
            "cluster_11": {"Race": "Race", "Sex": "Sex"},
        },
    },
    "cluster_17": {
        "cluster_14": {"Capital Gain": "Capital Gain", "Capital Loss": "Capital Loss"},
        "cluster_15": {"Hours per week": "Hours per week", "Country": "Country"},
    },
}

partition_tree = {
    "cluster_16": {
        "cluster_8": {"Age": "Age", "Race": "Race", "Sex": "Sex"},
    },
    "cluster_13": {
        "cluster_10": {
            "Occupation": "Occupation",
            "Hours per week": "Hours per week",
            "Relationship": "Relationship",
            "Education-Num": "Education-Num",
        },
        "cluster_14": {
            "Capital Gain": "Capital Gain",
            "Capital Loss": "Capital Loss",
            "Country": "Country",
        },
    },
}
partition_masker = shap.maskers.Partition(X.iloc[:50, :])

explainer = shap.explainers.Coalition(f, partition_masker, partition_tree=partition_tree)
row_to_explain = X.iloc[299:300, :]
winter_values = explainer(row_to_explain)

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 59ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step

CoalitionExplainer explainer: 2it [00:14, 14.75s/it]

[11]:

f(np.array(X.iloc[299:300, :]))

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 80ms/step

[11]:

array([0.23898253], dtype=float32)

[12]:

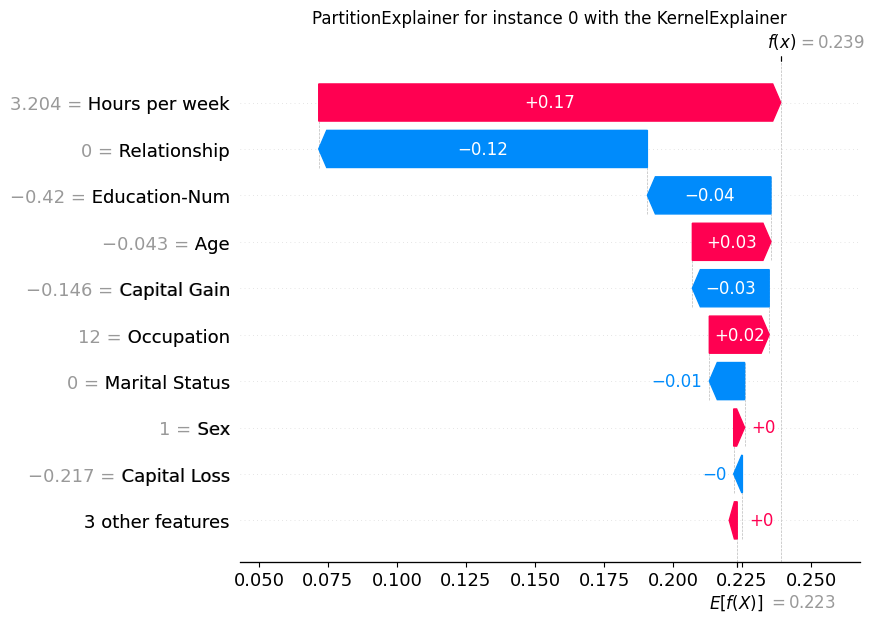
fig, ax = plt.subplots()
shap.plots.waterfall(shap_values[0], show=False)
plt.title("PartitionExplainer for instance 0 with the KernelExplainer")
plt.show()

../../../_images/example_notebooks_tabular_examples_neural_networks_Census_income_classification_with_Keras_17_0.png

[13]:

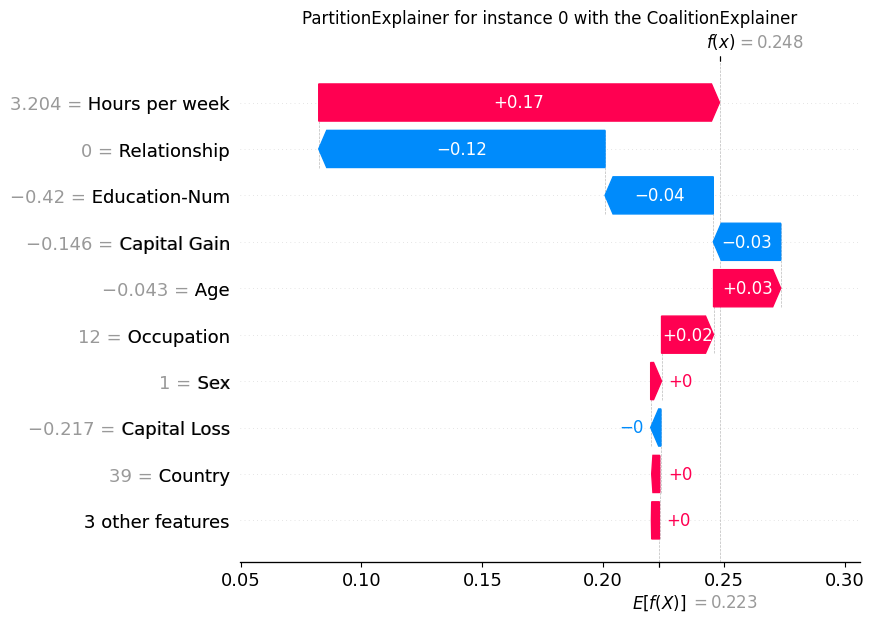
fig, ax = plt.subplots()
shap.plots.waterfall(winter_values[0], show=False)
plt.title("PartitionExplainer for instance 0 with the CoalitionExplainer")
plt.show()

../../../_images/example_notebooks_tabular_examples_neural_networks_Census_income_classification_with_Keras_18_0.png

[14]:

shap.initjs()
shap.force_plot(winter_values.base_values, winter_values.values, X_display.iloc[299:300, :])

[14]:

可视化已省略，Javascript 库未加载！
你是否已在此 notebook 中运行 `initjs()`？如果此 notebook 来自其他用户，你还必须信任此 notebook (文件 -> 信任 notebook)。如果你在 github 上查看此 notebook，则 Javascript 已为安全起见被剥离。如果你正在使用 JupyterLab，此错误是因为尚未编写 JupyterLab 扩展。

解释多个预测

在这里，我们为 20 个个体重复上述解释过程。由于我们使用的是基于采样的近似方法，每次解释可能需要几秒钟，具体取决于您的机器配置。

[15]:

winter_values50 = explainer(X.iloc[320:330, :])

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 67ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 67ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 61ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 91ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step

CoalitionExplainer explainer:  10%|█         | 1/10 [00:00<?, ?it/s]

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 15ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step

CoalitionExplainer explainer:  30%|███       | 3/10 [00:26<00:44,  6.36s/it]

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 14ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 15ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step

CoalitionExplainer explainer:  40%|████      | 4/10 [00:38<00:53,  8.83s/it]

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 59ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 72ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 112ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 60ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 58ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 59ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 50ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step

CoalitionExplainer explainer:  50%|█████     | 5/10 [00:55<00:58, 11.79s/it]

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step

CoalitionExplainer explainer:  60%|██████    | 6/10 [01:06<00:46, 11.56s/it]

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 74ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 15ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 57ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 15ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step

CoalitionExplainer explainer:  70%|███████   | 7/10 [01:18<00:35, 11.87s/it]

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 15ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 14ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 14ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 15ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 13ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 20ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step

CoalitionExplainer explainer:  80%|████████  | 8/10 [01:29<00:22, 11.44s/it]

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 12ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 74ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 15ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 23ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 24ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 27ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 25ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step

CoalitionExplainer explainer:  90%|█████████ | 9/10 [01:41<00:11, 11.51s/it]

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 55ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 28ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 178ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 73ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 22ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 17ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 19ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 18ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 36ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 16ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 50ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 39ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 21ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 64ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 50ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 54ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step

CoalitionExplainer explainer: 100%|██████████| 10/10 [01:57<00:00, 12.96s/it]

2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 29ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 50ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 35ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 64ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 50ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 50ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 49ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 30ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 37ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 41ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 40ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 54ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 44ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 53ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 78ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 45ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 54ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 34ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 31ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 52ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 38ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 33ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 63ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 46ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 42ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 43ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 32ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 47ms/step
2/2 ━━━━━━━━━━━━━━━━━━━━ 0s 48ms/step

CoalitionExplainer explainer: 11it [02:14, 13.49s/it]

[16]:

shap_values50 = kernel_explainer.shap_values(X.iloc[320:330, :], nsamples=500)

  0%|          | 0/10 [00:00<?, ?it/s]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 101ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step

 10%|█         | 1/10 [00:02<00:21,  2.41s/it]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 70ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step

 20%|██        | 2/10 [00:04<00:19,  2.40s/it]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 82ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step

 30%|███       | 3/10 [00:07<00:16,  2.41s/it]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 92ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step

 40%|████      | 4/10 [00:09<00:14,  2.46s/it]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 95ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step

 50%|█████     | 5/10 [00:12<00:12,  2.48s/it]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 93ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step

 60%|██████    | 6/10 [00:14<00:09,  2.48s/it]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 81ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 2s 2ms/step

 70%|███████   | 7/10 [00:16<00:07,  2.37s/it]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 51ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step

 80%|████████  | 8/10 [00:18<00:04,  2.07s/it]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 1s 2ms/step

 90%|█████████ | 9/10 [00:19<00:01,  1.94s/it]

1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 56ms/step
782/782 ━━━━━━━━━━━━━━━━━━━━ 1s 1ms/step

100%|██████████| 10/10 [00:21<00:00,  2.13s/it]

[17]:

shap.force_plot(kernel_explainer.expected_value, shap_values50, X_display.iloc[320:330, :])

[17]:

可视化已省略，Javascript 库未加载！
你是否已在此 notebook 中运行 `initjs()`？如果此 notebook 来自其他用户，你还必须信任此 notebook (文件 -> 信任 notebook)。如果你在 github 上查看此 notebook，则 Javascript 已为安全起见被剥离。如果你正在使用 JupyterLab，此错误是因为尚未编写 JupyterLab 扩展。

[18]:

shap.force_plot(winter_values50.base_values, winter_values50.values, X_display.iloc[320:330, :])

[18]:

可视化已省略，Javascript 库未加载！
你是否已在此 notebook 中运行 `initjs()`？如果此 notebook 来自其他用户，你还必须信任此 notebook (文件 -> 信任 notebook)。如果你在 github 上查看此 notebook，则 Javascript 已为安全起见被剥离。如果你正在使用 JupyterLab，此错误是因为尚未编写 JupyterLab 扩展。