使用 XGBoost 进行人口普查收入分类
这个 notebook 演示了如何使用 XGBoost 预测个人年收入超过 5 万美元的可能性。它使用了标准的 UCI Adult 收入数据集。要下载此 notebook 的副本,请访问 github。
梯度提升机方法(如 XGBoost)对于使用多种模态表格样式输入数据的此类预测问题是最先进的。Tree SHAP (arXiv 论文) 允许精确计算树集成方法的 SHAP 值,并且已直接集成到 C++ XGBoost 代码库中。这允许快速精确计算 SHAP 值,无需抽样且无需提供背景数据集(因为背景是从树的覆盖率推断出来的)。
在这里,我们演示如何使用 SHAP 值来理解 XGBoost 模型预测。
[1]:
import matplotlib.pylab as pl
import numpy as np
import xgboost
from sklearn.model_selection import train_test_split
import shap
# print the JS visualization code to the notebook
shap.initjs()
加载数据集
[2]:
X, y = shap.datasets.adult()
X_display, y_display = shap.datasets.adult(display=True)
# create a train/test split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=7)
d_train = xgboost.DMatrix(X_train, label=y_train)
d_test = xgboost.DMatrix(X_test, label=y_test)
训练模型
[3]:
params = {
"eta": 0.01,
"objective": "binary:logistic",
"subsample": 0.5,
"base_score": np.mean(y_train),
"eval_metric": "logloss",
}
model = xgboost.train(
params,
d_train,
5000,
evals=[(d_test, "test")],
verbose_eval=100,
early_stopping_rounds=20,
)
[0] test-logloss:0.54663
[100] test-logloss:0.36373
[200] test-logloss:0.31793
[300] test-logloss:0.30061
[400] test-logloss:0.29207
[500] test-logloss:0.28678
[600] test-logloss:0.28381
[700] test-logloss:0.28181
[800] test-logloss:0.28064
[900] test-logloss:0.27992
[1000] test-logloss:0.27928
[1019] test-logloss:0.27935
经典特征归因
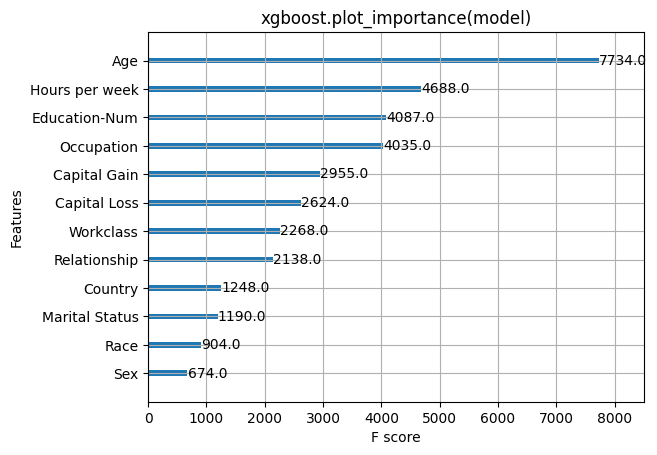
在这里,我们尝试 XGBoost 自带的全局特征重要性计算。请注意,它们彼此矛盾,这促使我们使用 SHAP 值,因为 SHAP 值具有一致性保证(意味着它们将正确地对特征进行排序)。
[4]:
xgboost.plot_importance(model)
pl.title("xgboost.plot_importance(model)")
pl.show()
[5]:
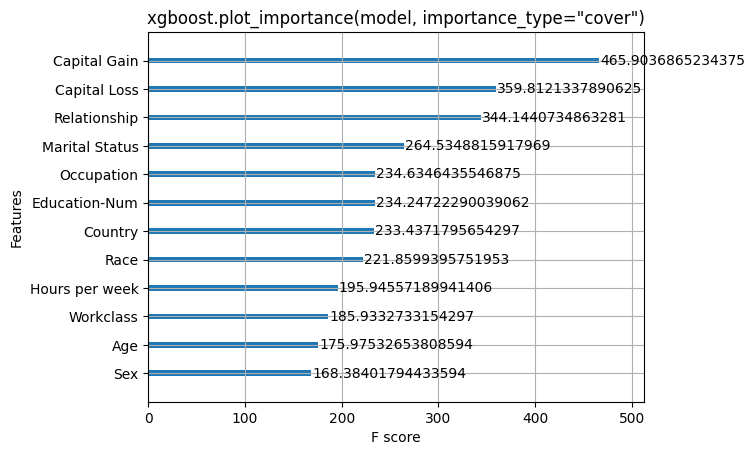
xgboost.plot_importance(model, importance_type="cover")
pl.title('xgboost.plot_importance(model, importance_type="cover")')
pl.show()
[6]:
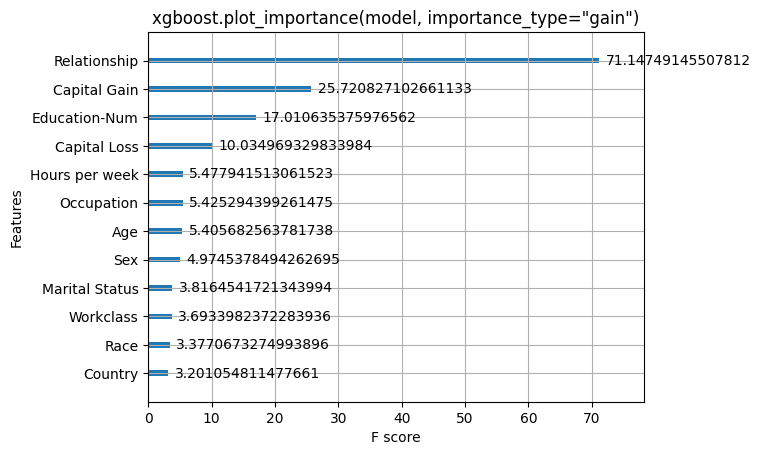
xgboost.plot_importance(model, importance_type="gain")
pl.title('xgboost.plot_importance(model, importance_type="gain")')
pl.show()
解释预测
在这里,我们使用集成到 XGBoost 中的 Tree SHAP 实现来解释整个数据集(32561 个样本)。
[7]:
# this takes a minute or two since we are explaining over 30 thousand samples in a model with over a thousand trees
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X)
可视化单个预测
请注意,我们使用 “display values” 数据帧,以便获得友好的字符串而不是类别代码。
[8]:
shap.force_plot(explainer.expected_value, shap_values[0, :], X_display.iloc[0, :])
[8]:
你是否在此 notebook 中运行了 `initjs()`?如果此 notebook 来自其他用户,你还必须信任此 notebook(文件 -> 信任 notebook)。如果你在 github 上查看此 notebook,则 Javascript 已被剥离以确保安全。如果你正在使用 JupyterLab,则此错误是因为尚未编写 JupyterLab 扩展。
可视化多个预测
为了保持浏览器流畅,我们仅可视化 1,000 个个体。
[9]:
shap.force_plot(explainer.expected_value, shap_values[:1000, :], X_display.iloc[:1000, :])
[9]:
你是否在此 notebook 中运行了 `initjs()`?如果此 notebook 来自其他用户,你还必须信任此 notebook(文件 -> 信任 notebook)。如果你在 github 上查看此 notebook,则 Javascript 已被剥离以确保安全。如果你正在使用 JupyterLab,则此错误是因为尚未编写 JupyterLab 扩展。
平均重要性条形图
这取数据集中 SHAP 值幅度的平均值,并将其绘制为简单的条形图。
[10]:
shap.summary_plot(shap_values, X_display, plot_type="bar")
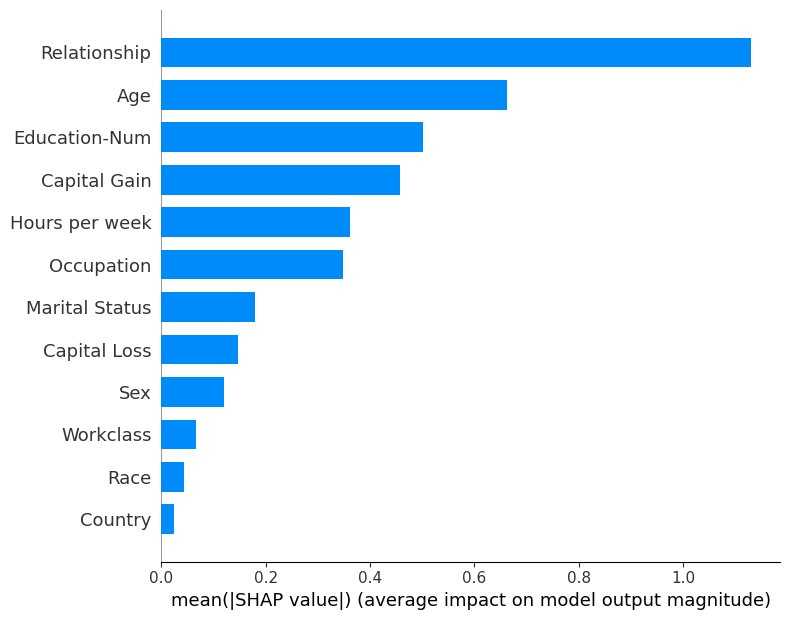
SHAP 汇总图
我们没有使用典型的特征重要性条形图,而是使用每个特征的 SHAP 值的密度散点图来识别每个特征对验证数据集中个体的模型输出的影响程度。特征按所有样本中 SHAP 值幅度的总和排序。有趣的是,relationship 特征比 capital gain 特征具有更大的总体模型影响,但是对于那些 capital gain 很重要的样本,它比 age 具有更大的影响。换句话说,capital gain 对少量预测产生很大影响,而 age 对所有预测产生较小影响。
请注意,当散点未落在一条线上时,它们会堆积以显示密度,并且每个点的颜色代表该个体的特征值。
[11]:
shap.summary_plot(shap_values, X)
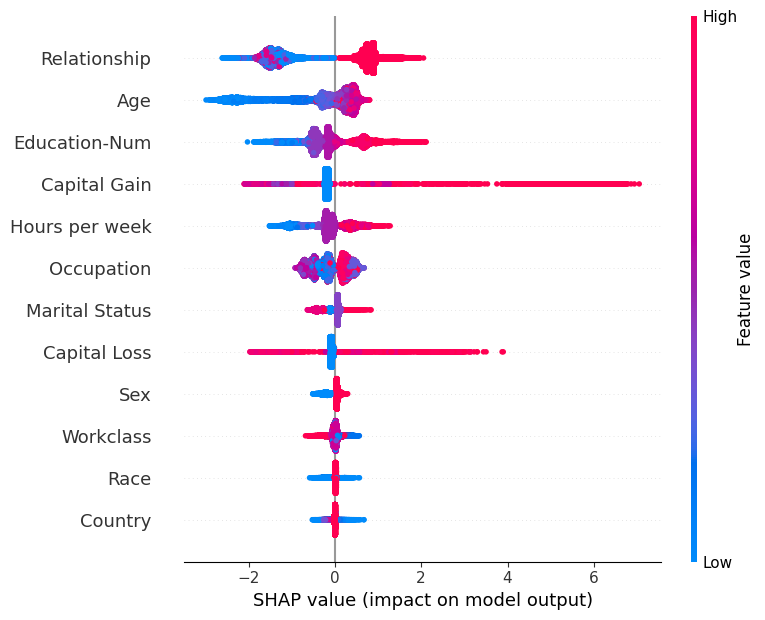
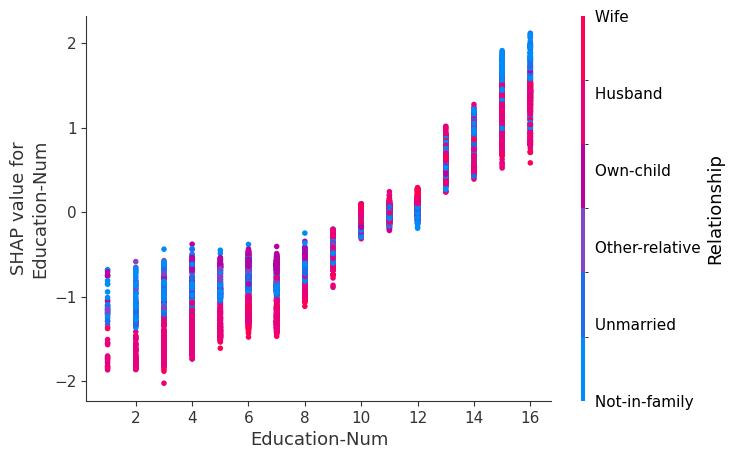
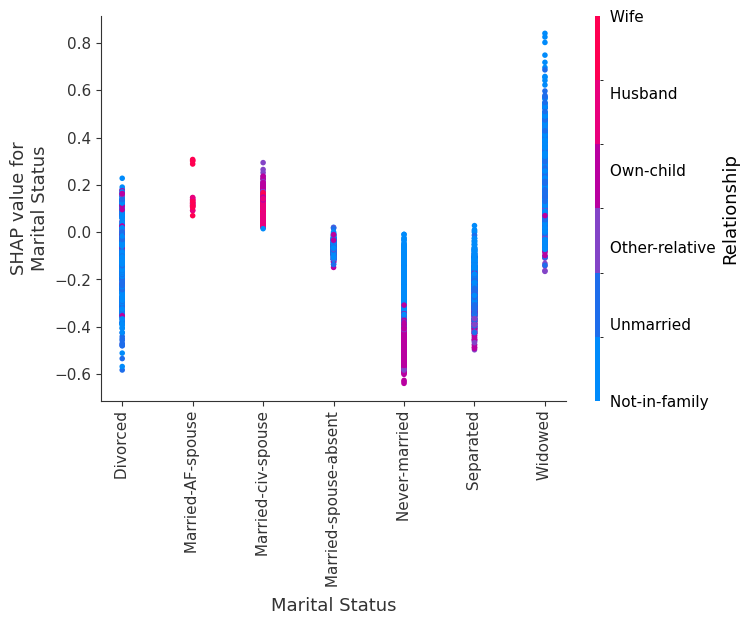
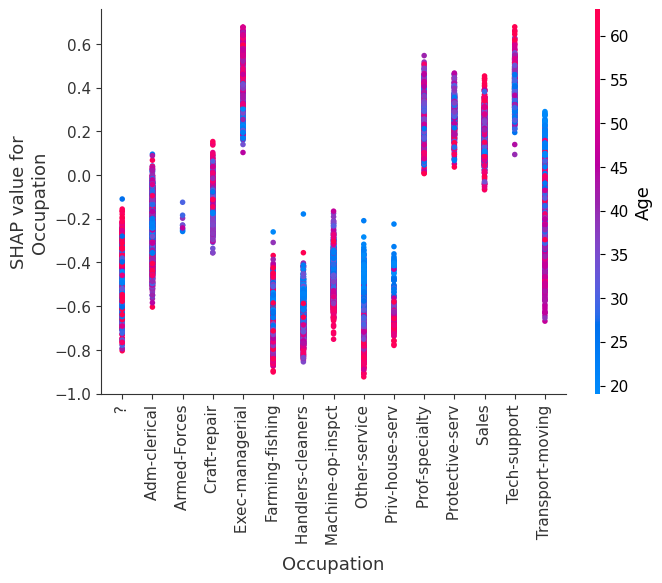
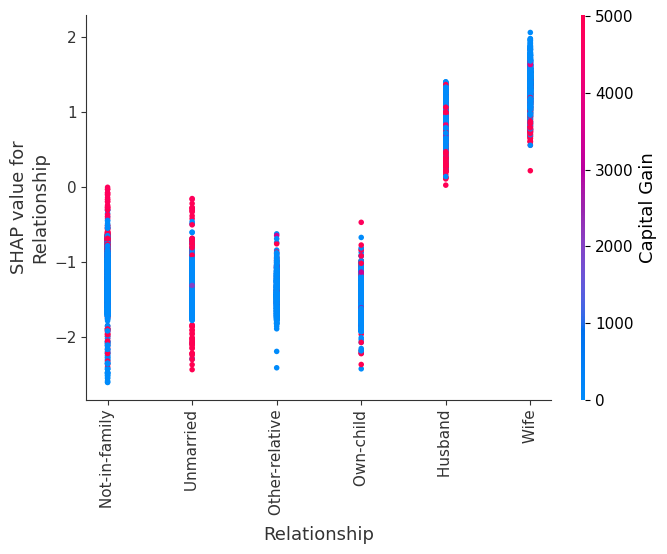
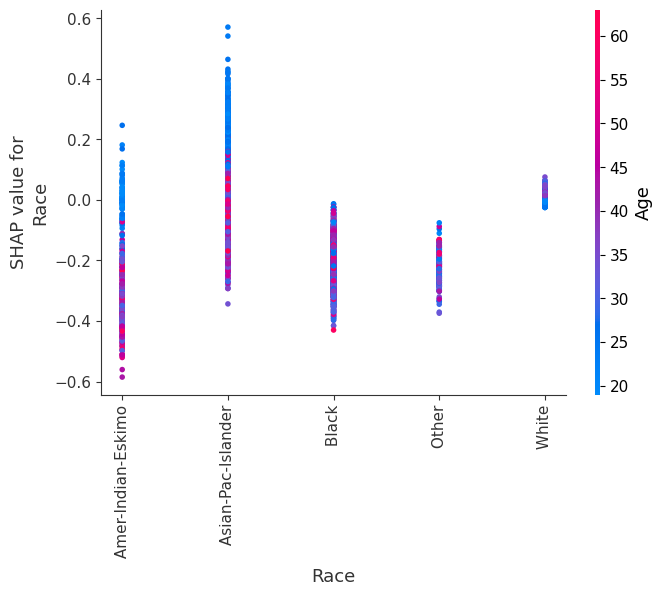
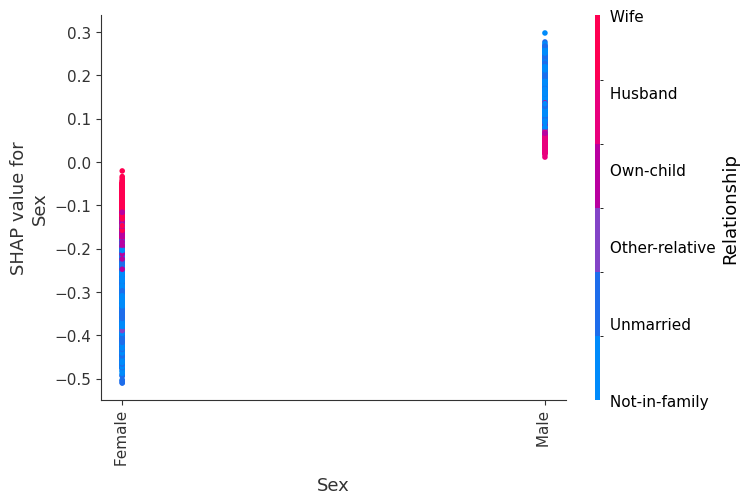
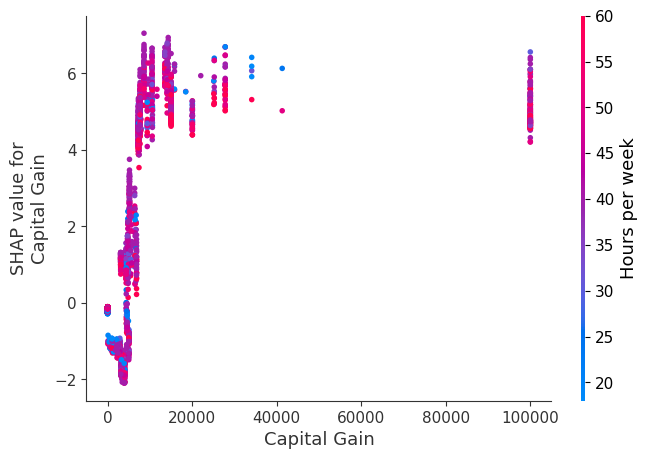
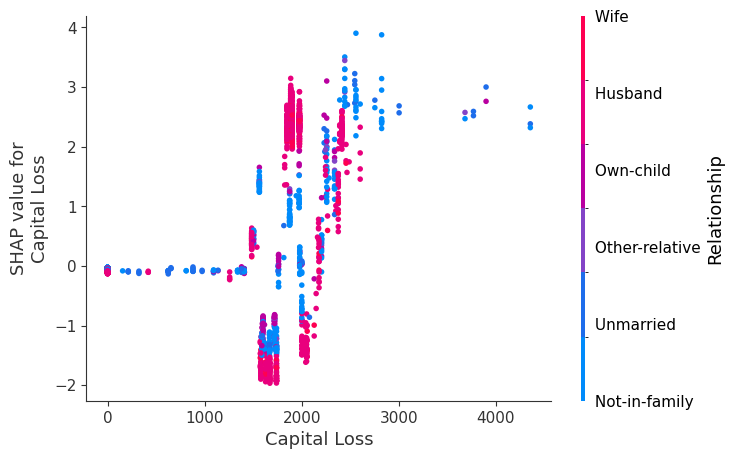
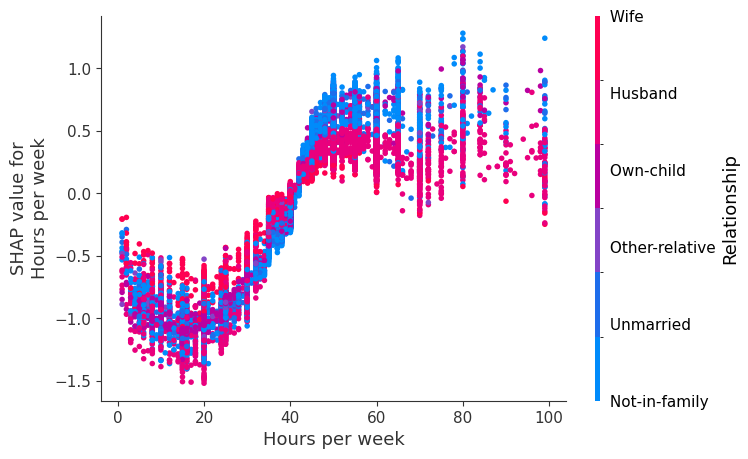
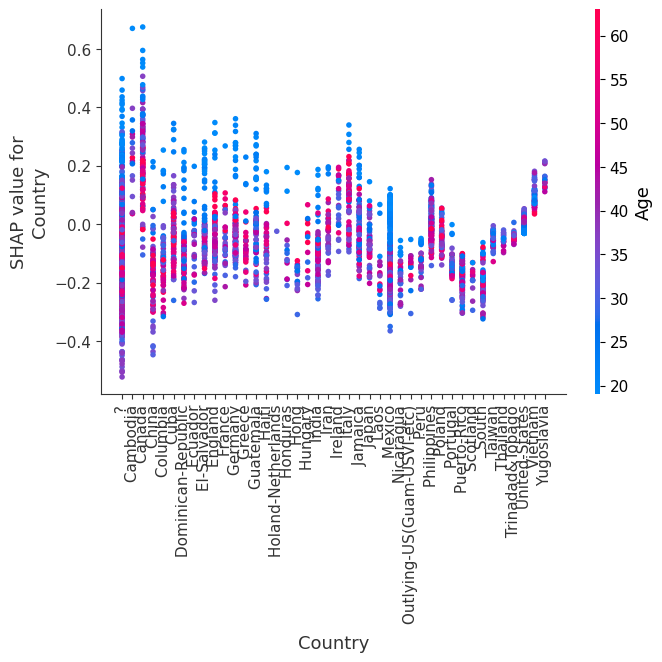
SHAP 依赖图
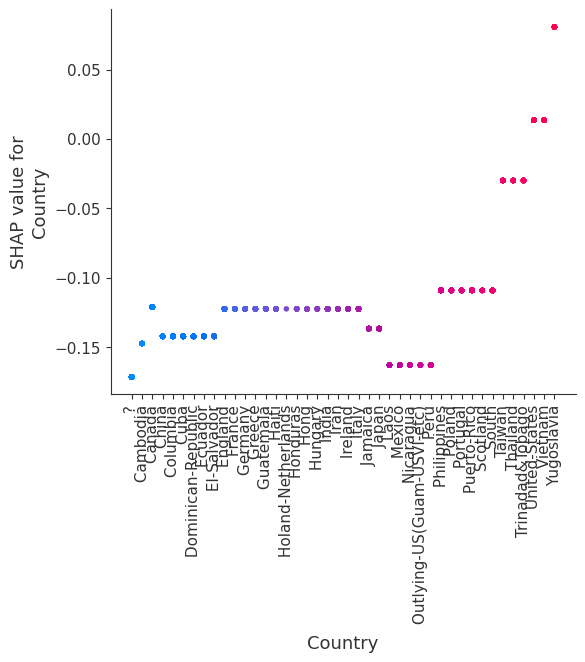
SHAP 依赖图显示单个特征在整个数据集上的影响。它们绘制了许多样本中特征的值与该特征的 SHAP 值。SHAP 依赖图类似于部分依赖图,但考虑了特征中存在的交互效应,并且仅在数据支持的输入空间区域中定义。单个特征值处 SHAP 值的垂直离散是由交互效应驱动的,并且选择另一个特征进行着色以突出可能的交互。
[12]:
for name in X_train.columns:
shap.dependence_plot(name, shap_values, X, display_features=X_display)
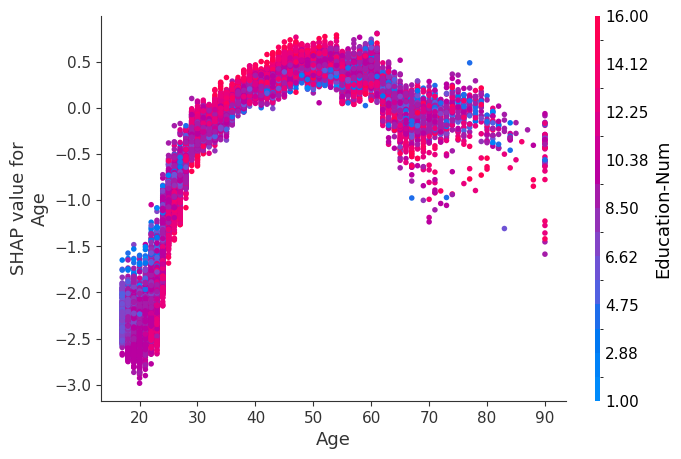
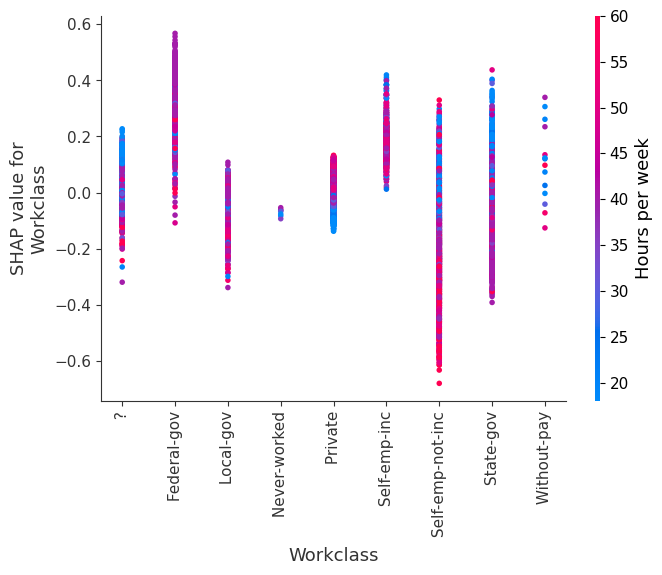
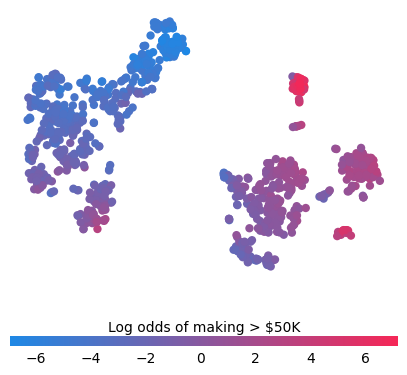
简单监督聚类
通过 shap_values 对人进行聚类,可以得到与手头预测任务相关的组(在本例中为他们的赚钱潜力)。
[13]:
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
shap_pca50 = PCA(n_components=12).fit_transform(shap_values[:1000, :])
shap_embedded = TSNE(n_components=2, perplexity=50).fit_transform(shap_values[:1000, :])
[14]:
from matplotlib.colors import LinearSegmentedColormap
cdict1 = {
"red": (
(0.0, 0.11764705882352941, 0.11764705882352941),
(1.0, 0.9607843137254902, 0.9607843137254902),
),
"green": (
(0.0, 0.5333333333333333, 0.5333333333333333),
(1.0, 0.15294117647058825, 0.15294117647058825),
),
"blue": (
(0.0, 0.8980392156862745, 0.8980392156862745),
(1.0, 0.3411764705882353, 0.3411764705882353),
),
"alpha": ((0.0, 1, 1), (0.5, 1, 1), (1.0, 1, 1)),
} # #1E88E5 -> #ff0052
red_blue_solid = LinearSegmentedColormap("RedBlue", cdict1)
[15]:
f = pl.figure(figsize=(5, 5))
pl.scatter(
shap_embedded[:, 0],
shap_embedded[:, 1],
c=shap_values[:1000, :].sum(1).astype(np.float64),
linewidth=0,
alpha=1.0,
cmap=red_blue_solid,
)
cb = pl.colorbar(label="Log odds of making > $50K", aspect=40, orientation="horizontal")
cb.set_alpha(1)
cb.outline.set_linewidth(0)
cb.ax.tick_params("x", length=0)
cb.ax.xaxis.set_label_position("top")
pl.gca().axis("off")
pl.show()
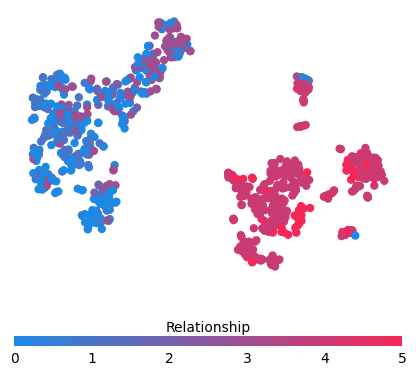
[16]:
for feature in ["Relationship", "Capital Gain", "Capital Loss"]:
f = pl.figure(figsize=(5, 5))
pl.scatter(
shap_embedded[:, 0],
shap_embedded[:, 1],
c=X[feature].values[:1000].astype(np.float64),
linewidth=0,
alpha=1.0,
cmap=red_blue_solid,
)
cb = pl.colorbar(label=feature, aspect=40, orientation="horizontal")
cb.set_alpha(1)
cb.outline.set_linewidth(0)
cb.ax.tick_params("x", length=0)
cb.ax.xaxis.set_label_position("top")
pl.gca().axis("off")
pl.show()
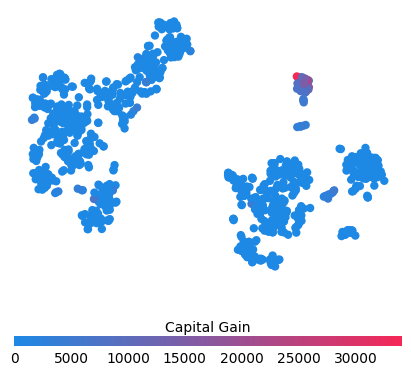
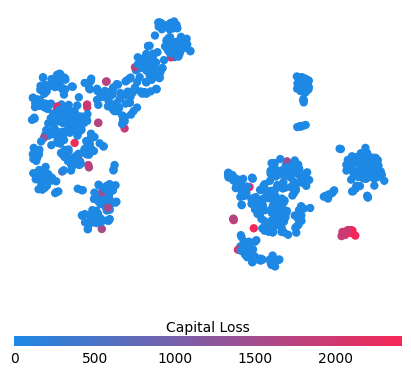
训练一个每个树只有两个叶子的模型,因此特征之间没有交互项
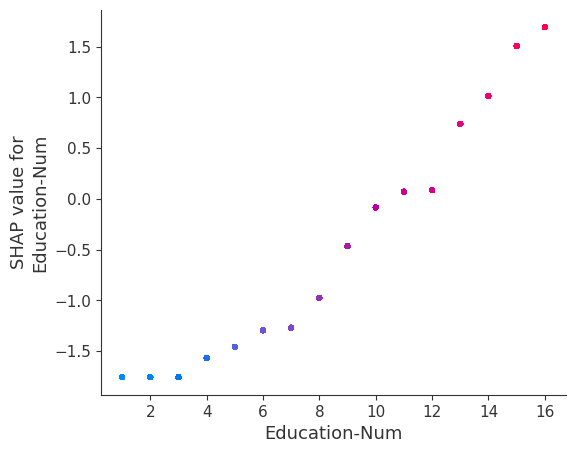
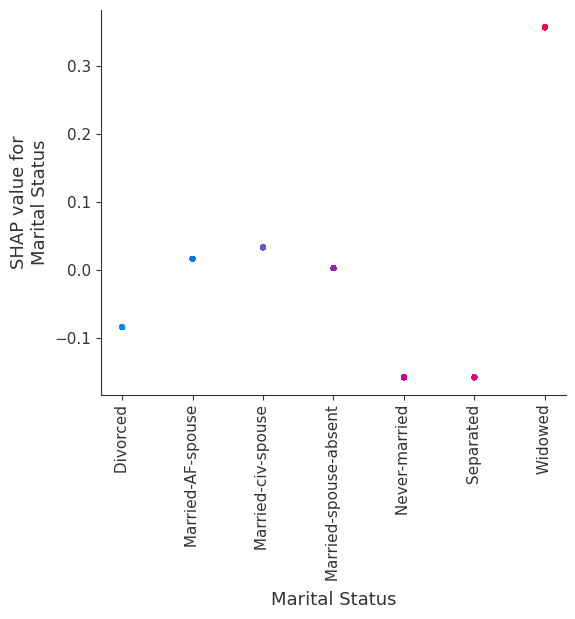
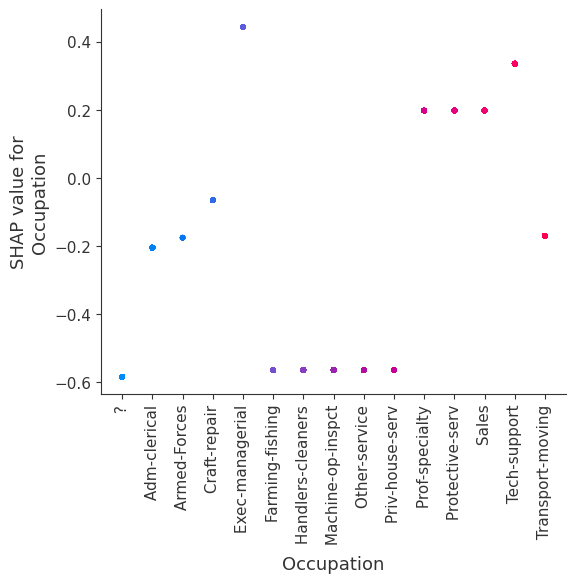
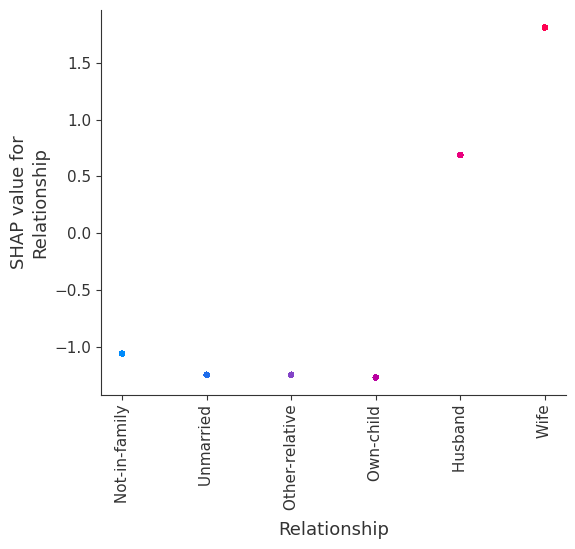
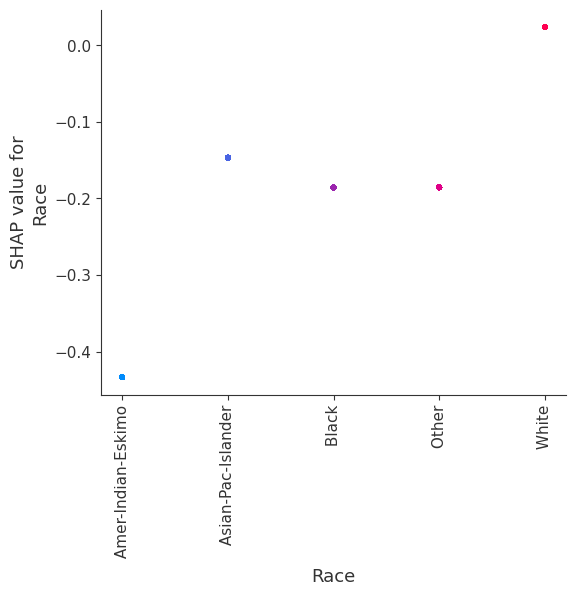
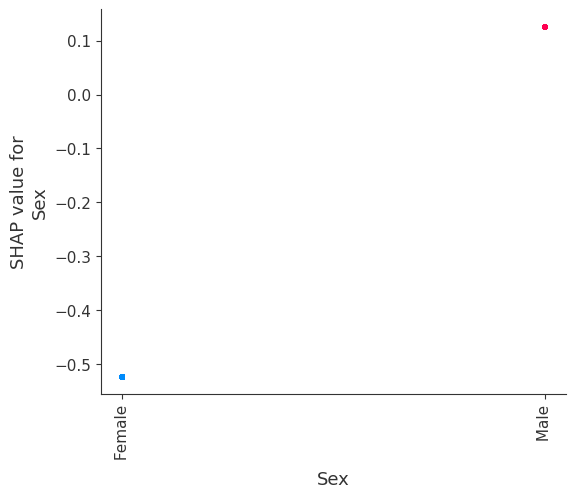
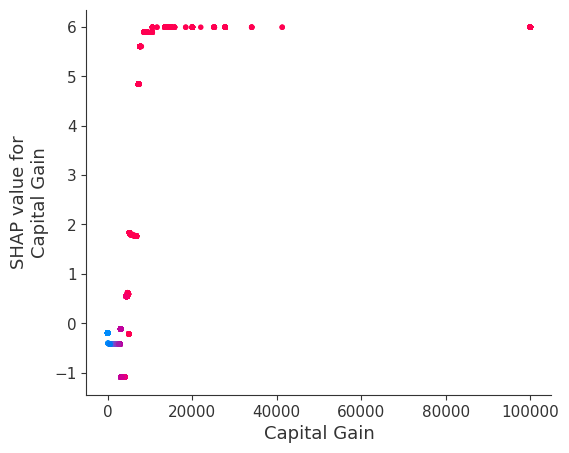
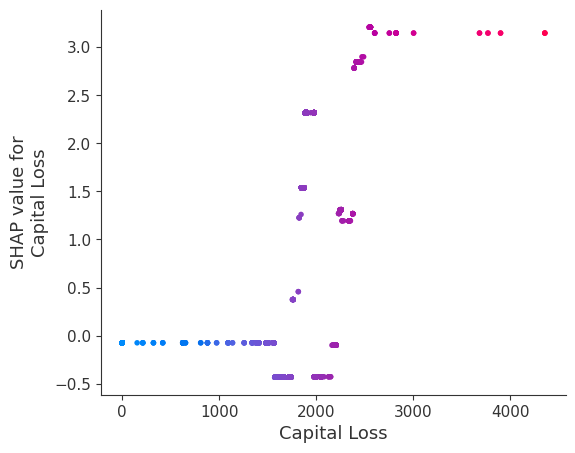
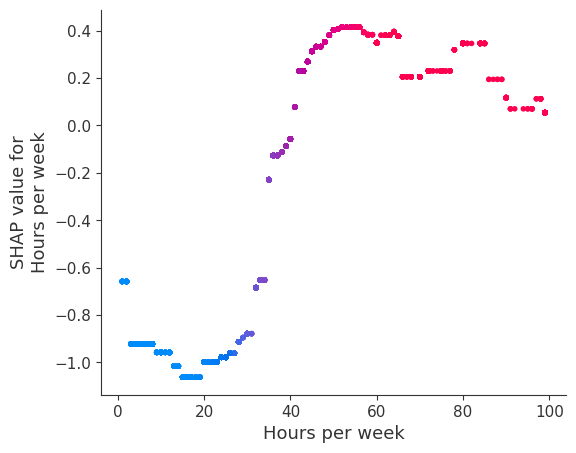
强制模型没有交互项意味着特征对结果的影响不依赖于任何其他特征的值。这在下面的 SHAP 依赖图中反映为没有垂直散布。垂直散布反映了单个特征值可能对模型输出产生不同的影响,具体取决于个体存在的其他特征的上下文。但是,对于没有交互项的模型,无论个体可能具有哪些其他属性,特征始终具有相同的影响。
SHAP 依赖图相对于传统部分依赖图的优势之一是能够区分具有和不具有交互项的模型。换句话说,SHAP 依赖图通过给定特征值处散点图的垂直方差,给出了交互项大小的概念。
[17]:
# train final model on the full data set
params = {
"eta": 0.05,
"max_depth": 1,
"objective": "binary:logistic",
"subsample": 0.5,
"base_score": np.mean(y_train),
"eval_metric": "logloss",
}
model_ind = xgboost.train(
params,
d_train,
5000,
evals=[(d_test, "test")],
verbose_eval=100,
early_stopping_rounds=20,
)
[0] test-logloss:0.54113
[100] test-logloss:0.35499
[200] test-logloss:0.32848
[300] test-logloss:0.31901
[400] test-logloss:0.31331
[500] test-logloss:0.30930
[600] test-logloss:0.30619
[700] test-logloss:0.30371
[800] test-logloss:0.30184
[900] test-logloss:0.30035
[1000] test-logloss:0.29913
[1100] test-logloss:0.29796
[1200] test-logloss:0.29695
[1300] test-logloss:0.29606
[1400] test-logloss:0.29525
[1500] test-logloss:0.29471
[1565] test-logloss:0.29439
[18]:
shap_values_ind = shap.TreeExplainer(model_ind).shap_values(X)
请注意,下面的交互颜色条对于此模型没有意义,因为它没有交互。
[19]:
for name in X_train.columns:
shap.dependence_plot(name, shap_values_ind, X, display_features=X_display)
invalid value encountered in divide
invalid value encountered in divide
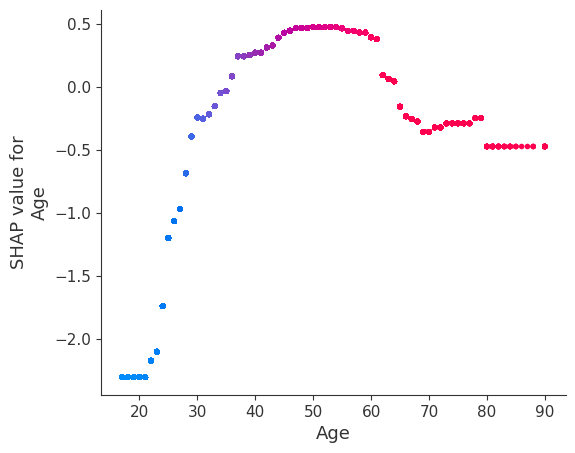
invalid value encountered in divide
invalid value encountered in divide
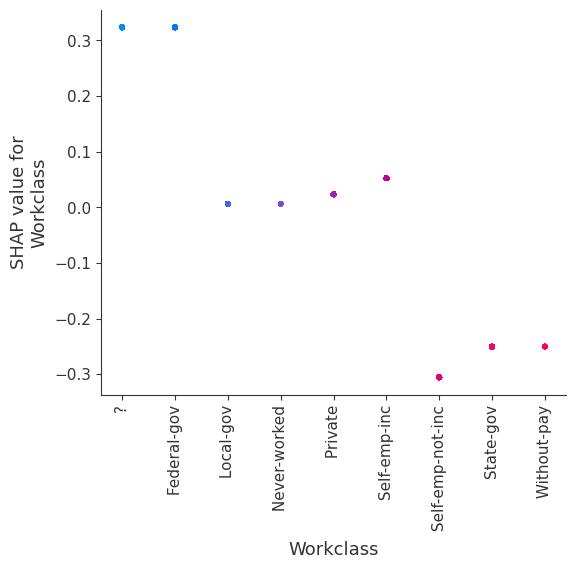
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide
invalid value encountered in divide